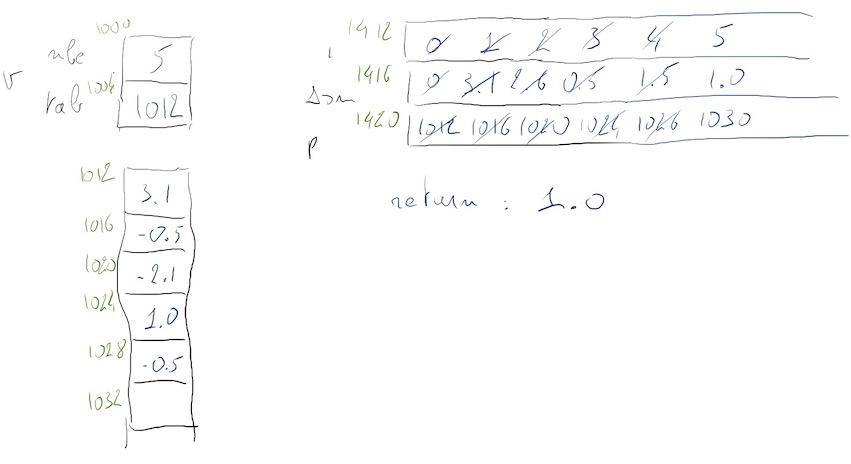Rmi Nollet et Jean-Jacques BOURDIN
- Universit Paris 8
-
Labo IA, Dpt. Informatique
- 2, rue de la Libert
- 93526 Saint-Denis Cedex
- FRANCE
Spring 2021
La semaine du 5 avril est consacre vos projets.
Donc pas de cours, mais nous rpondrons sans doute aux mails.
Le 13 avril vous prsentez vos projets. Peut-tre le 14 aussi,
si ce n'est pas fini.
Les partiels auront lieu le 20 avril, salle B104
15h, et le 11 mai 15h.
Vous ne pouvez pas participer aux deux partiels.
The C Language
Le Langage C
History, qualities, problems, future...
Quand, pourquoi, pourquoi pas, jusqu' quand, qui, qu'est-ce...
Organisation du Cours
About this course
Class + Lab
Cours + TP
Two written tests, one project (by pairs of students)
Deux partiels, un projet faire en binmes.
Bibliographie sommaire
- Le langage C - 2e d - Norme ANSI, Kernighan et Ritchie (Dunod)
- Mthodologie de la programmation en C - 4me dition, Jean-Pierre Braquelaire (dit Achille)
Some bindings will help you to use emacs. You'll find some at
this page , you can also type, within emacs,
Esc x and "describe-bindings".
Une srie de raccourcis est disponible sous
emacs, vous en trouverez d'autres en tapant
Esc x puis "describe-bindings" sous emacs.
- square
int square (int n) {
return n * n;
}
|
-
You can try cube, double, triple...
This function has to be linked to another one, the most important
one: the main function.
Cette fonction doit tre accompagne de celle qui la commande, la
grande fonction, la principale, main.
Both will be inside a simple file:
L'ensemble sera crit et plac dans un
fichier :
cours190119.c.
- A file
int square (int n) {
return n * n;
}
int main () {
printf("le carre de 3 est %d\n",square(2));
}
|
- to Compile
Then you have to translate this file to machine language. Our compiler is called gcc.
Il faut ensuite traduire ce texte en langage machine. Notre
traducteur (compilateur) se nomme gcc:
otake: cat cours190119.c
int square (int n) {
return n * n;
}
main () {
printf("le carre de 3 est %d\n",square(2));
}
otake: gcc cours190119.c
otake: ls -l
-rw-r--r-- 1 jj users 103 Jan 18 18:06 cours190119.c
-rwxr-xr-x 1 jj users 12264 Jan 18 18:07 a.out
|
- and execute
otake: a.out
le carre de 3 est 4 |
You may correct a semantic error.
Vous pouvez corriger afin d'arriver une phrase plus logique.
"S'il fait laid droite, je prends gauche" (Michel de Montaigne)
You might need to do something if a certain condition is met. For
example you don't take the road if there is a no entry sign.
Parfois il est ncessaire d'agir de faon diffrencie, d'o
le if.
/* which one is bigger? */
int maxi2 (int a, int b) {
if ( a < b ) {
return b;
}
else {
return a;
}
}
|
Vous devez crire :
- la fonction qui trouve le plus grand parmi trois nombres entiers ;
- la fonction qui trouve le plus grand parmi quatre nombres entiers ;
- la fonction qui trouve le plus petit parmi cinq nombres entiers ;
- la fonction qui trouve le second plus grand parmi trois nombres entiers ;
- la fonction qui trouve le second plus grand parmi quatre nombres entiers ;
sec4(7,3,2,9)==7
- la fonction qui trouve le second plus grand parmi cinq nombres entiers ;
Be careful
Every time one wants to use the recursivity, one has to follow the
following steps:
- Find an example with an easy to find result.
- Find a general rule, recursive.
- Verify that the general rule tends to the easy solution.
Attention :
Toute formulation rcursive doit suivre les tapes suivantes :
- Trouver un cas particulier dont la valeur est donne.
- Trouver une rgle gnrale qui donne une solution partir d'elle-mme.
- Vrifier que cette rgle gnrale rapproche du cas particulier.
Example: a function to compute the sum of the first numbers to n.
Une fonction qui calcule la somme des premiers entiers jusqu' n :
som(n) = 0 + 1 + 2 + 3 + ... + (n-1) + n
At first we find a number n, with its result
Un n avec son rsultat
som(0) = 0
Then we find a general formula:
Nous trouvons d'abord une formulation rcursive de cette suite :
som(n) = 0 + 1 + 2 + 3 + ... + (n-1) + n
som(n-1) = 0 + 1 + 2 + 3 + ... + (n-1)
Therefore
som(n) = som (n-1) + n
The general term is closer to the individual than the previous one
(n-1 is closer to 0 than n, the convergence is proved as n is a natural).
We have now a general case and a singular case, the general case tends forward to the singular one.
Il y a bien un cas particulier et une rgle gnrale. La rgle gnrale rapproche du cas particulier.
int som (int n) {
if ( n < 1 ) {
return 0;
}
else {
return n + som (n-1);
}
}
|
Vous devez crire :
- Somme des carrs des n premiers entiers
- Somme des cubes des n premiers entiers
- Somme des puissance quatre des n premiers entiers
- Produit des n premiers entiers
- Produit des carrs des n premiers entiers
- Produit des cubes des n premiers entiers
- Produit des puissances quatre des n premiers entiers
- Exponentiation (x puissance n)
- Somme des puissances p des n premiers entiers
sompn(2,4) = 0^4 + 1^4 + 2^4 = 17
- Additions par incrmentations successives
On suppose ne savoir faire des additions que de +1 ou -1.
L'addition de deux valeurs add(a+b) peut tre ramene l'addition de a+1 et celle de b-1 n'est-ce pas ?
crivez la fonction rcursive qui fait ainsi l'addition de deux valeurs.
- Soustractions de deux valeurs
Ici encore avec uniquement des +1 et -1.
- Multiplication russe
Il s'agit de faire la multiplication par additions successives.
- Division entire et rcursive
- Reste de la Division entire
- Plus grand diviseur commun de deux entiers
- Plus petit multiple commun de deux entiers
- Pour trouver l'entier x suprieur ou gale la racine
carre d'un nombre a, il suffit de passer en revue tous les
entiers jusqu' avoir dpass la racine.
Faites la fonction C
correspondante.
- Vous venez de trouver un nombre x suprieur ou gal la
racine carre d'un autre nombre a. Vous savez donc que x et x-1
encadrent la racine. Faire une fonction qui renvoie celle de ces
deux valeurs qui est la plus proche de la racine.
Of course you'll need also the main function to test all these functions.
Avec, bien sr, une fonction main qui appelle et affiche les rsultats
des prcdentes.
Note that you're not allowed to use not already presented functions or tools.
Attention, ce qui n'a pas encore t vu ne doit pas tre utilis.
Tout programme non test est rput faux.
If you don't try it, it doesn't work.
Si vous voulez d'autres exercices, il suffit de demander...
Example for the second of four numbers if function little of four
values (ltt4) is already known.
Exemple pour le second parmi 4, si on connait dj la fonction
pluspetit de 4 ltt4 :
int sec4_2_aux (int a, int b, int c, int d, int min) {
if (a == min)
return sec3(b, c, d);
if (b == min)
return sec3(a, c, d);
if (c == min)
return sec3(a, b, d);
return sec3(a, b, c);
}
int sec4_2 (int a, int b, int c, int d) {
return sec4_2_aux(a, b, c, d,ltt4 (a, b, c, d));
}
|
You should know about Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21...
A formulation can be given as:
La suite de Fibonacci est connue pour sa forte progression. Les
premires valeurs sont calcules par :
f(0) = 1
f(1) = 1
f(n) = f(n-1) + f(n-2)
Just write the program and test it.
Vous pouvez maintenant tester cette suite clbre.
Il faut la programmer et essayer diffrentes valeurs. On doit obtenir :
1 1 2 3 5 8 13 21 34 55 89 144
You always must verify the convergence of a recursive formula.
La question de la convergence d'une formule rcursive doit toujours
tre pose et rsolue avant la programmation. Elle repose sur une
mthode simple :
- Find a boundary value.
- In the general term,
- verify that the argument of the call is
closer to the boundary value than the initial term. If it's in
discrete maths, then the convergence is met.
- vrifier l'existence d'une borne, c'est--dire d'une situation de fin,
- dans la formule rcursive, vrifier que le nouvel appel est plus
prs de la fin que la formule prcdente
- vrifier que ce rapprochement est discret (si on avance de 1 en 1
vers 0, partir d'une valeur entire, on va, certainement y
arriver).
Example Fibonacci.
Two boundaries are given, f(0) and f(1).
In the general term, to compute f(n) one needs to compute f(n-1) and
f(n-2). These values are closer to 0 and 1 than n. n, n-1, n-2 are
integers therefore it converges.
Exemple, pour Fibonacci, il y a deux valeurs de fin, f(0) et f(1).
Dans la formule rcursive, partir d'un certain n, (on
cherche calculer f(n)), on doit calculer f(n-1) et
f(n-2) donc le paramtre est plus prs de 0 ou 1 que le
n initial. Comme ces valeurs sont discrtes, on arrive
forcment l'une des bornes.
A function is tail recursive is the recursive call is the last
thing to be evaluated by the function.
On parle de rcursivit terminale lorsque l'appel rcursif est la
dernire action de la fonction, c'est--dire lorsque le rsultat
obtenu par cet appel est le rsultat de la fonction appelante.
Exemple :
som (int n) {
if (n == 0) {
return 0;
}
else {
return n + som (n-1);
}
}
|
This function is clearly not tail-recursive as when som(n-1) will be
known, an addition will be computed.
n'est pas rcursif terminal : aprs l'obtention du rsultat de
som(n-1) il faut encore faire une addition avec ce rsultat.
Par contre,
int somrec (int n) {
return somrec_aux (n,0);
}
int somrec_aux (int n, int s) {
if (n <= 0) {
return s;
}
else {
return somrec_aux (n-1, s+n);
}
}
|
est rcursif terminal. Il faut, le plus souvent, transmettre non
seulement le paramtre, mais aussi un accumulateur (ici
s), chaque appel de fonction.
To obtain a tail-recursive function, one has to add an accumulator
argument which store the computation and tends to the solution.
Voici un exemple de fonction main pour tester somrec :
main () {
printf("som(%d)==\t%d\n",4,somrec(4));
printf("som(%d)==\t%d\n",5,somrec(5));
printf("som(%d)==\t%d\n",6,somrec(6));
}
|
We'll try now with the multiplcation.
Essayons avec autre chose. Par exemple la multiplication par additions
successives. La formule globale est :
m(a,0) = 0
m(a,b) = b + m(a-1,b)
This expression is an addition so the neutral element is 0. The
accumulator starts then at 0.
L'opration principale est ici une addition. Son lment neutre
est 0. L'accumulateur commencera 0.
The general term is :
Si on veut faire, au fur et mesure, ces additions, il
faut, chaque tape, ajouter b.
M(a,b,som) = M(a-1,b,som+b)
One can see that the third argument starts with 0 than 0+b, then 0+b+b
and so on.
Dans ce cas, petit petit, on va se diriger vers a valant 0 et
le troisime argument valant b+b+b+...+b (en tout, a(initial) fois).
Comme ce troisime argument reoit des valeurs en les ajoutant, il
convient de lui donner une valeur initiale nulle.
int mulrecter (int a, int b) {
return mulrecter_aux (a, b, 0);
}
int mulrecter_aux (int a, int b, int som) {
if (a == 0) {
return som;
}
else {
return mulrecter_aux (a-1, b, som + b);
}
}
|
Exercices
You have to write every recursive function done earlier in a tail
recursive form. The Fibonacci sequence has to be done also as tail recursive.
Reprendre les fonctions prcdentes (somme, produit, puissance,
Fibonacci...) et les programmer en utilisant la rcusivit terminale.
- Variables
A variable is a tuple of three elements: <name, type, address>
One needs to declare the variables ASAP in the function. Then they can
be set by the operator = (pronounce "receive").
Une variable est un triplet : (nom, type, espace mmoire).
La taille de l'espace mmoire est dfinie par le type comme vu
ci-dessus. On peut modifier le contenu de l'espace mmoire par
l'opration d'affectation.
/* les autres fonctions ne sont pas cites */
main () {
int max; /* sert plusieurs fois */
max = 10;
printf("%d \t=> \t %d\n",max, serie(max));
max = 50;
printf("%d \t=> \t %d\n",max, serie(max));
max = 100;
printf("%d \t=> \t %d\n",max, serie(max));
max = 500;
printf("%d \t=> \t %d\n",max, serie(max));
max = 1000;
printf("%d \t=> \t %d\n",max, serie(max));
}
|
- Expressions
Here after you'll find examples of expressions:
On parlera d'expression pour dcrire un ensemble de formules que l'on peut valuer base
d'oprateurs "bien construits" et excutables. Exemples :
3 + 5 * 6
(3 + 5) * 6
6 * 9 / 5
|
And examples of non-expressions:
Par contre
N'en sont pas.
- Types
- Principle :
Everything must be declared and associated with a
type of objects. Each type is associated with a number of
functionnalities and a size that is the number of bytes it needs in
the memory.
Principe : Tout objet doit tre dclar avec un type qui signifie ce
qu'il est. Chaque type est associ un certain nombre de
fonctionnalits et une taille reserve en machine.
| type |
taille | genre |
| void |
0 | vide |
| char |
≥1 | caractre |
| short |
≥2 | entier " court " |
| long (ou int) |
≥4 | entier "long" |
| float |
≥4 | nombre virgule |
| double |
≥8 | nombre virgule, plus prcis |
| long long int |
≥8 | entier "trs long " |
| long double |
≥16 | nombre virgule prcis |
Examples
Quelques exemples d'utilisation.
3/2 donne 1
( 3 * 2.0 ) / 5 donne 1.2
|
- Casting
Cast demand ou cast implicite ?
Exemple :
float inverse (int n) {
if (n == 0.0) {
return 0.0;
}
else {
return (1.0 / (float) n);
}
}
int serie (int n) {
if (n == 0) {
return 0;
}
else {
return inverse(n) + serie (n-1);
}
}
main () {
printf("%d \t=> \t %d\n",10, serie(10));
printf("%d \t=> \t %d\n",50, serie(50));
printf("%d \t=> \t %d\n",100, serie(100));
printf("%d \t=> \t %d\n",1000, serie(1000));
}
/* ------------------ Essai -----------------
otake: a.out
10 => 1
50 => 1
100 => 1
500 => 1
1000 => 1
---------------------------------------------*/
|
Strange isn't it?
Il s'agit donc d'une srie terriblement convergente (elle
est constante)
de valeur 1.
Corrigez-la.
Donnez la sous forme rcursive terminale.
- Statement
A statement is a ";", or an expression followed by an
instruction (therefore with a ";" at
the end).
Une instruction est soit ";", soit une expression suivie
d'une instruction (donc aussi de
";")
A statement may also be presented as a { followed by a } and
containing only valable statements.
Une instruction peut aussi tre prsente comme un ensemble
d'instructions entoures par des accolades. On parle alors de bloc.
- Arity/Arit
- Associativity/Associativit
- Returned value/Valeur renvoye
- Priority/Priorit des oprateurs en C
| Operator | Associativity
| Arity |
() []
-> . | GD | - |
| ! ~ ++ -- + - | DG | 1 |
| * & (type) sizeof | DG | 1 |
| * / % | GD | 2 |
| + - | GD | 2 |
| << >> | GD | 2 |
| < <= > >= | GD | 2 |
| == != | GD | 2 |
| & | GD | 2 |
| ^ | GD | 2 |
| | | GD | 2 |
| && | GD | 2 |
| || | GD | 2 |
| ? : | DG | 3 |
= += -= *= /= %=
<<= >>= &= ^= |= | DG | 2 |
| , | GD | 2 |
II.C) Flow control
Structures de Contrle
II.C.1) Montaigne
"S'il fait laid droite, je vais gauche."
Dj vu.
Il faut simplement remarquer qu'il est possible d'enchaner les if et
les else, c'est mme parfois plus joli (mais plus logique ?).
int fibifif (int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 1;
}
else {
return fibifif(n-1) + fibifif(n-2);
}
}
}
|
II.C.2) Pink Floyd
If I were to sleep, I could dream
If I were afraid, I could hide
If I go insane, please don't put
Your wires in my brain
Just another "if"?
Il s'agit d'un if tendu o la comparaison ne se passe que
sur la valeur "littrale". Exemple :
int fibsw (int n) {
switch (n) {
case 0:
return 1;
case 1:
return 1;
default:
return fibsw(n - 1);
}
}
|
Let's try another example:
void lecase (int n) {
switch (n) {
case 0:
printf("C est nul\n");
case 1:
printf("C est unique\n");
case 2:
printf("La paire\n");
case 3:
printf("La trinite\n");
}
printf("\n");
}
int main(){
lecase(5);
lecase(3);
lecase(1);
lecase(2);
lecase(0);
return 0;
}
|
What's that?
neige: a.out
La trinite
C est unique
La paire
La trinite
La paire
La trinite
C est nul
C est unique
La paire
La trinite
neige:
|
The "case"s are not working as "if then" but as entry point in a sequence.
II.C.3) Harrison
- while
While my guitar gently weeps (G. Harrison)
Trad. tant que ma guitare pleure doucement
While the condition stands, we do the work.
Tant que la condition est remplie, on fait ce qui suit.
int somw (int n) {
int i, som;
i = 0;
som = 0;
while (i < n) {
som = som + i;
i = i + 1;
}
return som;
}
|
- do while
C'est exactement la mme chose que le while, mais on ne fait le test
qu'aprs une premire itration.
int somdo (int n) {
int i, som;
i = 0;
som = 0;
do {
som = som + i;
i = i + 1;
} while (i < n);
return som;
}
|
Write with while or do-while each of the following fonctions:
Vous devez crire avec des whiles ou des do-while, donc en itratif :
- Somme des carrs des n premiers entiers
- Somme des cubes des n premiers entiers
- Somme des puissance quatre des n premiers entiers
- Produit des n premiers entiers
- Produit des carrs des n premiers entiers
- Produit des cubes des n premiers entiers
- Produit des puissances quatre des n premiers entiers
- Exponentiation (x puissance n)
- Somme des puissances p des n premiers entiers
sompn(2,4) = 0^4 + 1^4 + 2^4 = 17
- Additions par incrmentations successives
On suppose ne savoir faire des additions que de +1 ou -1.
L'addition de deux valeurs add(a+b) peut tre ramene l'addition de a+1 et celle de b-1 n'est-ce pas ?
crivez la fonction rcursive qui fait ainsi l'addition de deux valeurs.
- Soustractions de deux valeurs
Ici encore avec uniquement des +1 et -1.
- Multiplication russe
Il s'agit de faire la multiplication par additions successives.
- Division entire et rcursive
- Reste de la Division entire
- Plus grand divieur commun de deux entiers
- Plus petit multiple commun de deux entiers
- Une fonction main qui appelle et affiche les rsultats
des prcdentes
II.C.4) Halley
- Principle
for is almost like while but for initial, and ending parts.
For, c'est exactement la mme chose que while part que les
instructions d'avant (l'initialisation) et de fin de boucle (incrmentation) sont, en
gnral, incluses dans les "paramtres" de l'instruction.
First example, the computation of the sum of the n first integer numbers.
Premier
exemple, le calcul de la somme des n premiers entiers :
int somf (int n) {
int i, som;
i = 0;
som = 0;
for (/* void_1*/ ; i < n; /* void_2*/ ) {
som = som + i;
i = i + 1;
}
return som;
}
|
Dans ce cas le "for" est un "while".
- Deuxime exemple :
int somf2 (int n) {
int i, som;
/*void_1*/
som = 0;
for ( i = 0 ; i < n; i = i + 1 ) {
som = som + i;
/* void_2 */
}
return som;
}
|
- Exercices
Don't hesitate to write again your recursive functions with a for.
Il faut, ce stade, reprendre une partie de la liste des fonctions
(sommes, factorielles, exponentiation, y compris Fibonacci) avec
des for.
II.C.5)Percy Mayfield
Special statements
Instructions d'chappement
- return
Dj vu.
Return exits from the function when it's executed.
- break
Break exits from a control flow. Examples:
Pour interrompre une itration (sortir de la structure de
contrle). Exemples :
int sombr (int n) {
int i, s;
i = 0;
s = 0;
while (1) {
s = s + i;
i = i + 1;
if (i > n) {
break;
}
}
return s;
}
|
int valeur (int n) {
int s;
s = 0;
switch (n) {
case 0:
s = 0;
case 1:
s = s + 1;
case 2:
s = s + 2;
case 3:
s = s + 3;
default:
s = s + n;
}
return s;
}
|
Qu'obtient-on aprs l'appel de :
valeur (2);
valeur (3);
valeur (1);
valeur (5);
Autre version, sans doute plus claire :
int valeur (int n) {
int s;
s = 0;
switch (n) {
case 0:
s = 0;
break;
case 1:
s = s + 1;
break;
case 2:
s = s + 2;
break;
case 3:
s = s + 3;
break;
default:
s = s + n;
break;
}
return s;
}
|
Tous les case doivent tre suivis d'un break ou,
sinon, d'un /*NOBREAK*/
- continue
Pour reprendre une itration (revenir la structure de
contrle). Exemple :
int fibstrange (int n) {
int i, prec, ante;
prec = 1;
ante = 1;
i = 0;
while (i <= n) {
i = i + 1;
if (i < 3) {
continue;
}
prec = prec + ante;
ante = prec - ante;
}
return prec;
}
|
Second exemple, o on voit que le continue passe bien l'itration
suivante :
#include <stdio.h>
int impair (int n) {
int i, res;
res = 0;
for (i = 0; i < n; i = i + 2)
;
return i - n;
}
int somp (int n) {
int s, i;
s = 0;
for (i=0; i <= n; i = i + 1) {
if (impair(i)) {
printf("%d est impair\n",i);
continue;
}
s = s + i;
}
return s;
}
int main () {
int a;
a = 5;
printf("Somme des pairs jusqu a %d : \t %d\n", a, somp(a));
a = 6;
printf("Somme des pairs jusqu a %d : \t %d\n", a, somp(a));
a = 7;
printf("Somme des pairs jusqu a %d : \t %d\n", a, somp(a));
}
|
- goto and label
Don't use it except for handling errors.
Le plus souvent utilis pour les gestions d'erreurs graves.
/* Just let's have mo'fun */
#include <stdlib.h>
#include <stdio.h>
int funct (int n) {
int a, b, c;
a = 1;
b = 1;
c = 2;
if (c > n) {
return a;
}
cas_general:
a = a + b;
b = a - b;
c = c + 1;
if (c <= n) {
goto cas_general;
}
return a;
}
int fonct (int n) {
int a, b;
a = 1;
b = 1;
do {
a = a + b;
b = a - b;
n = n - 1;
if (1 > n) {
goto cas_sortie;
}
} while(1);
cas_sortie:
return b;
}
int finct (int n) {
int a, b, c;
if (n > 23) {
a = -1;
goto la_sortie;
}
a = 1;
b = 1;
c = 2;
cas_retour:
if (c > n)
goto la_sortie;
a = a + b;
b = a - b;
c = c + 1;
goto cas_retour;
la_sortie:
return a;
}
main () {
int i;
for (i = 0; i < 10; i = i + 1) {
printf("Pour %d on a \t%d\t",i,funct(i));
printf("et\t %d ",fonct(i));
printf("et\t %d\n",finct(i));
}
}
|
Qui donne l'excution :
Pour 0 on a 1 et 1 et 1
Pour 1 on a 1 et 1 et 1
Pour 2 on a 2 et 2 et 2
Pour 3 on a 3 et 3 et 3
Pour 4 on a 5 et 5 et 5
Pour 5 on a 8 et 8 et 8
Pour 6 on a 13 et 13 et 13
Pour 7 on a 21 et 21 et 21
Pour 8 on a 34 et 34 et 34
Pour 9 on a 55 et 55 et 55
|
Pour l'instant, les labels et gotos ne fonctionnent que au sein d'une
fonction. Pour passer d'une fonction une autre, il faudra utiliser
les saut plus longs, les "long jump" (rendez-vous en Programmation
Imprative II).
- Quelques rappels
Other examples
#include <stdio.h>
float racine (float x) {
float y, pas;
pas = 0.0001;
y = 0.0; // initialisation
while ( 1 ) {
if ( y * y >= x) {
break;
}
y += pas; //incrmentation
}
/*
y = 0.0; // initialisation
while ( y * y < x) { // test
// printf(" %f ", y);
y += pas; //incrmentation
}
for (y = 0.0; y * y < x; y += pas) {
printf(" %f ", y);
}
*/
printf("\n");
return y;
}
int impair (int n) {
while (n > 1) {
n -= 2;
}
if (n==1) {
return 1;
}
return 0;
}
int sommepairs (int n) {
int i, somp;
somp = 0;
for (i = 0; i ≤ n; i++) {
if (impair(i)) {
continue;
}
somp = somp + i;
}
return somp;
}
int sommepairsgt (int n) {
int i, somp;
somp = 0;
i = 0;
debut_boucle:
if (impair(i)) {
goto incrementation;
}
somp += i;
incrementation:
i += 1;
if (i ≤ n) {
goto debut_boucle;
}
return somp;
}
int main () {
float val, rac;
int a, b, c;
val = 2.0;
rac = racine (val);
printf("la racine de %f est %f\n", val, rac);
for (a = 0; a < 10; a++) {
b = sommepairs(a);
c = sommepairsgt(a);
printf("jusqu a %d on a %d ou %d\n", a, b, c);
}
}
|
II.D.1)
Variables
A variable is a triplet : (name,type,location)(nom,type,lieu).
One needs to draw a variable with its box, where the value will be written.
Il convient donc de dessiner une variable avec sa "boite" associe.
The variable declarations have to be all in one place at the beginning
of the function.
Les dclarations doivent tre groupes en dbut de fonction. C'est
mme la premire chose faire lorsqu'on commence une fonction.
While lots of programmers don't apply that rule, lots of programmers
spend more time than necessary on debugging.
Si cette rgle n'est pas applique, ne vous tonnez pas de passer
plus de temps en debugging que les autres...
II.D.2) Enum
Enumration
Just to build a limited set of values, of any kind.
/* On va essayer de trouver deux exemples d enumeration */
enum sema {lundi, mardi, mercredi, jeudi, vendredi, samedi, dimanche};
enum week {sunday, monday, tuesday, wednesday, thursday, friday, saturday};
void affiche_day (enum week d) {
switch(d) {
case sunday:
printf("sunday");
break;
case monday:
printf("monday");
break;
case tuesday:
printf("tuesday");
break;
case wednesday:
printf("wednesday");
break;
case thursday:
printf("thursday");
break;
case friday:
printf("friday");
break;
case saturday:
printf("saturday");
break;
}
}
void affiche_jour (enum sema j) {
switch(j) {
case lundi:
printf("lundi");
break;
case mardi:
printf("mardi");
break;
case mercredi:
printf("mercredi");
break;
case jeudi:
printf("jeudi");
break;
case vendredi:
printf("vendredi");
break;
case samedi:
printf("samedi");
break;
case dimanche:
printf("dimanche");
break;
}
}
main () {
enum sema jour;
enum week day;
for (jour = lundi; jour <= dimanche; jour++) {
day = (enum day) jour;
affiche_day(day);
printf(" \t = \t");
affiche_jour(jour);
printf("\n");
}
}
/*
sunday = lundi
monday = mardi
tuesday = mercredi
wednesday = jeudi
thursday = vendredi
friday = samedi
saturday = dimanche
*/
|
You'll correct it, right?
Il va falloir agir, lundi n'est pas sunday !
#include <stdio.h>
enum boole {vrai, faux};
enum boole non (enum boole v) {
switch (v) {
case vrai : return faux;
case faux : return vrai;
}
}
enum boole et (enum boole v, enum boole w) {
if (v == faux)
return faux;
if (w == faux)
return faux;
return vrai;
}
enum boole ou (enum boole v, enum boole w) {
if (v == vrai)
return vrai;
if (w == vrai)
return vrai;
return faux;
}
void afficheb (enum boole v) {
if (v == vrai)
printf("vrai");
else
printf("faux");
printf(" ");
}
int main () {
enum boole a, b, c, d, e, f;
printf(" a\t b\t c\t et\t ou\t b+1\n");
f = 0;
for (a = vrai; a ≤ faux; a = a + 1) {
c = non (a);
for (b = vrai; b ≤ faux; b = b + 1) {
d = et (a, b);
e = ou (a, b);
f = f + 1;
printf("%2d\t %2d\t %2d\t %2d\t %2d\t %2d\t \n",a, b, c, d, e, f);
}
}
f = 0;
printf("\n a\t b\t c\t et\t ou\t b+1\n");
for (a = vrai; a ≤ faux; a = a + 1) {
c = non (a);
for (b = vrai; b ≤ faux; b = b + 1) {
d = et (a, b);
e = ou (a, b);
f = f + 1;
afficheb(a);
afficheb(b);
afficheb(c);
afficheb(d);
afficheb(e);
afficheb(f);
printf("\n");
}
}
printf(" Taille de cet enum : %d\n", (int) sizeof(enum boole));
}
|
II.D.3) Vectors
- Use
Premiers usages
Fill a vector with values
Objectif placer dans un vecteur toutes les valeurs de la somme des n
premiers entiers (pour tous les n).
int somvec (int n) {
int t [100];
int i;
t [0] = 0;
if (n > 99) {
return -1;
}
for (i=1; i <= n; i++) {
t[i] = t[i-1] + i;
}
return t[n];
}
int main () {
int v, res;
v = 5;
res = somvec(v);
printf("som(%d)=%d\n",v,res);
v = 6;
res = somvec(v);
printf("som(%d)=%d\n",v,res);
v = 7;
res = somvec(v);
printf("som(%d)=%d\n",v,res);
}
|
Second example:
Fill a vector with variable values
Second exemple :
Remplir un vecteur avec des valeurs quelconques.
#include<stdio.h>
void remplir (float vec [100], int nb) {
float x, eps;
int i;
if (nb >= 100)
return;
x = 1.5;
eps = 0.173;
for (i = 0; i < nb; i = i + 1) {
vec [i] = x;
x = x + eps;
if (x > 2.0)
eps = 0.01 - eps;
if (x < 0.5)
eps = 0.015 - eps;
}
}
void voirvec (float vec [100], int nb) {
int i;
if (nb >= 100)
return;
for (i = 0; i < nb; i = i + 1) {
printf("vec[%3d] == %f\n",i, vec [i]);
}
}
int main () {
int n;
float vec [100];
n = 20;
remplir(vec, n);
voirvec(vec, n);
}
|
The results are:
Donne ceci :
vec[ 0] == 1.500000
vec[ 1] == 1.673000
vec[ 2] == 1.846000
vec[ 3] == 2.019000
vec[ 4] == 1.856000
vec[ 5] == 1.693000
vec[ 6] == 1.530000
vec[ 7] == 1.367000
vec[ 8] == 1.204000
vec[ 9] == 1.041000
vec[ 10] == 0.878000
vec[ 11] == 0.715000
vec[ 12] == 0.552000
vec[ 13] == 0.389000
vec[ 14] == 0.567000
vec[ 15] == 0.745000
vec[ 16] == 0.923000
vec[ 17] == 1.101000
vec[ 18] == 1.279000
vec[ 19] == 1.457000
|
Another function, with integers this time.
Autre fonction de remplissage d'un vecteur, d'entiers cette fois.
void remplirv (int nb, int vec[100]) {
int crt, pre, new, i;
crt = 1;
pre = 1;
vec[0]=pre;
vec[1]=crt;
for (i=2; i <= n; i = 1 + i) {
new = (crt + pre) % 23; // reste de la division
vec[i] = new;
pre = crt;
crt = new;
}
}
|
- Liste d'exercices faire :
Refaire tous les exercices itratifs en remplissant un
vecteur au fur et mesure et en utilisant les valeurs dj
dans le vecteur pour calculer les nouvelles.
Coninuez avec :
- Faire une fonction qui affiche les lments du vecteur.
- Faire une fonction qui renvoie le nombre d'lments nuls du vecteur.
- Faire une fonction qui renvoie le nombre d'lments du vecteur gaux un certain x.
- Faire une fonction qui renvoie la premire valeur du vecteur qui soit le carr d'un entier ou -1 sinon.
- Faire une fonction qui renvoie la somme des valeurs du vecteur.
- Faire une fonction qui renvoie la somme des valeurs du vecteur infrieures x.
- Faire une fonction qui affiche les valeurs du vecteur dans l'ordre inverse.
- Faire une fonction qui renvoie la plus grande valeur du vecteur.
- Faire une fonction qui renvoie la plus petite valeur du vecteur.
- Faire une fonction qui renvoie la seconde plus petite valeur
du vecteur.
- Faire une fonction qui renvoie la moyenne des valeurs du vecteur.
- Faire une fonction qui replace les valeurs du vecteur dans l'ordre inverse.
- Faire une fonction qui renvoie la mdiane des valeurs du vecteur.
- Faire une fonction qui renvoie l'cart-type du vecteur.
- Fabriquez un autre vecteur dans lequel vous mettrez en premier
l'lment le plus grand lment du vecteur initial, puis en second
le second plus grand, puis le troisime et ainsi de suite,
le dernier lment du second vecteur sera le plus petit du vecteur
de dpart. Affichez le vecteur ainsi rang.
vecteur initial : [8, 13, 21, 11, 9, 20, 6, 3, 9, 12]
Vecteur final : [21, 20, 13, 12, 11, 9, 9, 8, 6, 3]
- Faire une fonction qui insre une valeur dans un vecteur rang en ordre dcroissant.
insere([1,2,6,9,10],5,8) donne un vecteur de 6 lments : [1,2,6,7,8,9,10].
- Faire une fonction qui trie le vecteur dans l'ordre dcroissant grce la fonction ci-dessus.
- With letters
Avec des textes
Let's replace lower case letters with upper case letters in a text.
Et si nous nous amusions remplacer les minuscules par des
majuscules
dans un texte ?
/* jjb */
void replaceminparmaj (int nbc, char txt [1000]) {
int i, diff;
if (nbc > 999) {
printf("\n\ntrop de texte\n\n");
return;
}
for (i = 0; i < nbc; i++) {
diff = txt[i] - 'a';
if (diff >= 0) {
if (diff < 26) {
txt[i] = (char) ('A' + diff);
}
}
}
}
void affitxt (int nbc, char t [1000]) {
int i;
for (i= 0; i < nbc; i++) {
printf("%c",t[i]);
}
printf("\n");
}
void remplirtxt (int nbc, char t [1000]) {
int i;
for (i=0; i < 50; i++) {
t[i] = (char) 'a' + (i % 26);
}
for (i=50; i < 60; i++) {
t[i] = ' ';
}
for (i=60; i < 110; i++) {
t[i] = (char) 'A' + (i % 26);
}
for (i=110; i < nbc; i++) {
t[i] = ' ';
}
}
/* on peut utiliser ce remplissage aussi */
int remplirchaine(char ch [1000]) {
ch [0] = 'J';
ch [1] = 'e';
ch [2] = ' ';
ch [3] = 'F';
ch [4] = 'a';
ch [5] = 'i';
ch [6] = 's';
ch [7] = ' ';
ch [8] = 'S';
ch [9] = 'o';
ch [10] = 'u';
ch [11] = 'v';
ch [12] = 'e';
ch [13] = 'n';
ch [14] = 't';
ch [15] = ' ';
ch [16] = '\0';
return 16;
}
int main () {
int nbc;
char t [1000];
nbc = 120;
remplirtxt(nbc,t);
affitxt(nbc, t);
replaceminparmaj(nbc, t);
affitxt(nbc, t);
nbc = remplirchaine(t);
affitxt(nbc, t);
replaceminparmaj(nbc, t);
affitxt(nbc, t);
}
}
|
Just try it.
Il ne reste plus qu' essayer :
neige: gcc ex16.c
neige: a.out
abcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwx IJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTUVWXYZABCDEF
ABCDEFGHIJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTUVWX IJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTUVWXYZABCDEF
Je Fais Souvent
JE FAIS SOUVENT
|
As one might see, you always associate the number of elements of a
vector to the vector itself when it is passed as argument.
Remarquez bien que quand on veut transmettre un vecteur comme argument
il est trs important de transmettre aussi le nombre d'lments
utiliss de ce vecteur.
A little bit more: a function to fill a vector and a function to see
its elements.
Quelques fonctions de vecteurs supplmentaires, une fonction de
remplissage et une d'affichage, pour des vecteurs de nombres entiers.
- Soit un vecteur de caractres. Un mot est dfini par des
caractres et est spar des autres mots par un ou des signes de
ponctuation (virgule, point, espace...). Compter le nombre de mots
d'un vecteur de caractres. Pour ceci vous pouvez utilisez la
fonction de remplissage ci-dessous.
void remplirc (int nbc, char vc [1000]) {
int i, j, k;
char c;
c = 'a';
j = 3;
k = 1;
for (i = 0; i < nbc; i = i + 1) {
vc[i] = c ;
c = c + j;
if (c > 'z') {
c = ' ';
}
else {
if (c < 'a') {
c = 'a' + k;
k = k + 1;
}
}
if (k > 10) {
k = 2;
}
}
}
void affichechars (int nbc, char vc [1000]) {
int i;
printf(" Les caracteres sont\n");
for (i = 0; i < nbc; i = i + 1) {
printf ("%c",vc[i]);
}
printf("\n");
}
|
We'll need typedef to help us understand.
Nous rajoutons ici la commande "typedef" qui permet de dfinir
un nouveau type donnes partir des types dj connus.
typedef float tablef [100];
Et, au lieu d'crire partout float t [100] on crira
tablef t.
Two Dimensions table
Tableaux deux dimensions
A table is only a vector of vectors.
Un tableau deux dimensions est simplement un vecteur de vecteurs.
exemple :
Example
Nous allons travailler avec des tableaux d'altitude. Sur une grande
carte, carre, nous donnons l'altitude de chacune des cases,
c'est--dire l'altitude moyenne pour toute la surface
qu'elle reprsente sur le terrain.
Pour gnrer le tableau, il faut utiliser cette fonction en donnant
comme paramtres, le tableau, le nombre de colonnes et le nombre de
lignes :
/* exo sur les altitudes JJ'2012 */
typedef float table [100] [100];
/* desormais table est un synonyme de float [100][100]*/
void remplirt (table t, int sx, int sy) {
int x, y, sxy;
float v, eps, add, pas;
pas = 0.5;
v = pas;
add = 5.0;
sxy = sx * sx + sy * sy;
eps = 1.0 / (float) (sxy);
for (x = 0; x < sx; x += 1) {
for (y = 0; y < x; y += 1) {
t[x][y] = (float) (x * x - y * y + add) * eps;
}
for (y = x; y < sy; y += 1) {
t[x][y] = (float) ( y * y - x * x + add) * eps;
}
add += v;
if (add > 10.0)
v = - pas;
if (add < 0.1)
v = pas;
}
}
|
Nous pouvons donc maintenant utiliser une fonction pour afficher ce
tableau et la fonction main pour s'en servir.
Note : le dnivel entre deux points et la diffrence d'altitude entre ces deux points.
Un dnivel positif est un dnivel dont la valeur est positive.
Puis
- Trouver le point culminant (la valeur la plus grande) d'une certaine ligne horizontale.
- Trouver le point culminant d'une certaine colonne.
- Trouver le point culminant de toute la surface.
- Trouver le second point culminant de toute la surface.
- Calculer le dnivel entre deux points donns.
- Calculer la somme des dnivels entre deux points
d'une ligne. Il faut donc que le numro de la ligne soit fourni en argument.
- Calculer la somme des dnivels entre deux points
d'une colonne. Il faut donc que le numro de la colonne soit fourni en argument.
- Calculer la somme des dnivels positifs entre deux
points
le long d'une ligne.
- Calculer la somme des dnivels ngatifs entre deux
points
le long d'une colonne.
Tableaux trois, quatre dimensions, ou plus
Il suffit d'tendre les connaissances pour imaginer la suite.
/* exo sur les tableaux a trois dimensions */
typedef float table3 [50] [50] [50];
void remplirt (table3 t, int sx, int sy, int sz) {
int x, y, sxy, z;
float v, eps, add, pas;
pas = 0.5;
v = pas;
add = 5.0;
sxy = sx * sx + sy * sy;
eps = 1.0 / (float) (sxy);
for (x = 0; x < sx; x += 1) {
for (y = 0; y < x; y += 1) {
for (z = 0; z < sz; z += 1) {
t[x][y][z] = (float) (x * x - y * y + z + add) * eps;
}
}
for (y = x; y < sy; y += 1) {
for (z = 0; z < sz; z += 1) {
t[x][y][z] = (float) ( y * y - x * x + z + add) * eps;
}
}
add += v;
if (add > 10.0)
v = - pas;
if (add < 0.1)
v = pas;
}
}
|
II.D.4) Structures
A structure is a set of variables of possibly different types.
Nous dfinissons des structures comme tant des assemblages d'objets
diffrents, contrairement au tableau qui est un assemblage d'objets du
mme type.
- Definition
Dfinition et exemple simple
struct duo {
int quot;
int rest;
} ;
typedef struct duo duo;
|
Just use it.
Nous avons donc maintenant dfini une structure compose de deux
entiers, utile pour renvoyer le reste et le quotient d'une division.
duo division (int a, int b) {
duo d;
d.quot = 0;
d.rest = 0;
if (b == 0)
return d;
while (a >= b) {
a = a - b;
d.quot = d.quot + 1;
}
d.rest = a;
return d;
}
|
int main () {
duo res;
int a, b;
res = division(a,b);
printf(" when dividing %d by %d, one gets a result of %d with a
reminder of %d\n", a, b, res.quot, res.rest);
}
|
- Definition 2
Dfinition 2
All the type definitions are to be placed at the start of the file, in the "head" of the file.
On place toujours la dfinition en tte de fichier
Vous trouverez ci-dessous une dclaration permettant de systmatiser
les tableaux d'altitudes, avec non seulement les valeurs, mais aussi
les largeurs et hauteurs de la table.
Example:
Nous mettons en place une structure de vecteur de nombres entiers.
struct vecint {
int nbele;
int vec[100];
};
typedef struct vecint vecint_t;
|
Il faut videmment modifier la fonction qui remplit ce vecteur :
vecint_t remplirv (int nb) {
int crt, pre, new, i;
vecint_t w;
crt = 1;
pre = 1;
w.vec[0]=pre;
w.vec[1]=crt;
for (i=2; i <= nb; i = 1 + i) {
new = (crt + pre) % 23; // reste de la division
w.vec[i] = new;
pre = crt;
crt = new;
}
w.nbele = nb;
return w;
}
|
Refaire quelques exercices de vecteurs d'entiers avec cette structure.
New example:
struct table_alt {
int larg;
int haut;
float t[100][100];
};
typedef struct table_alt table_alt_t;
|
Now the word "t_table_alt" is defined as a type of objects composed of
two integers and a table of float numbers.
Maintenant t_table_alt est un mot reserv dont la signification est :
"objet compos de deux entiers et un tableau de flottants".
Reprendre quelques exercices avec ces tableaux et les crire en
utilisant la structure ad hoc.
table_alt_t remplirt (int sx, int sy) {
int x, y, sxy;
float v, eps, add, pas;
table_alt_t tt;
tt.larg = sx;
tt.haut = sy;
pas = 0.5;
v = pas;
add = 5.0;
sxy = sx * sx + sy * sy;
eps = 1.0 / (float) (sxy);
for (x = 0; x < sx; x += 1) {
for (y = 0; y < x; y += 1) {
tt.t[x][y] = (float) (x * x - y * y + add) * eps;
}
for (y = x; y < sy; y += 1) {
tt.t[x][y] = (float) ( y * y - x * x + add) * eps;
}
add += v;
if (add > 10.0)
v = - pas;
if (add < 0.1)
v = pas;
}
return tt; /* ici on doit renvoyer la structure */
}
|
- Utilisation
Il ne reste plus qu' utiliser cette structure avec ces valeurs pour faire les autres exercices.
- Square root
Dtour par la racine
How to find the square root of a positive number x? It's the number,
say y, that respects y * y == x.
La racine carre, y, d'un nombre virgule, x, est difficile trouver.
C'est le nombre qui, multipli par lui-mme, donne x.
x == y * y
If x≥0 then 0≤ y <x+ 1.
Commenons
par cette constatation : si ce nombre, x, est positif ou nul
alors la racine est comprise entre 0 et x+1, toujours.
Let's call inf and sup these values (0 and
x+1). Let's call med the average of them. it is easy to find
if y is greater than med or not. If y>med then y belongs to
]med,sup], if not, y belongs to [inf, med]. One just has to set one of
the two values inf or sup and carry on, and on, and on...
When does it stop? When the value is close enough to the square
root. Close enough is when the difference is smaller than a given value.
Mais entre ces deux valeurs, inf et sup, il y en a
beaucoup. Coupons par le
milieu, mil. Comment savoir si la racine est plus grande ou
plus petite que mil ? Et si elle est plus petite, ne
pouvons-nous pas rduire l'intervalle de recherche ? De mme si
elle est plus grande.
Vous pouvez faire tourner longtemps cet algorithme, mais attention,
vous n'avez pas besoin d'une infinit de chiffres, il faut donc vous
arrter quand la prcision requise est acquise !
Write this function square root.
Faites une fonction qui calcule ainsi la racine carre d'un nombre positif virgule.
- Complex numbers.
As seen in class a structure for complex numbers can be:
struct complex {
float real;
float imag;
};
typedef struct complex complex;
|
A function to add two complex numbers is given by:
struct complex mulc (struct complex a, struct complex b) {
struct complex res;
res.real = a.real + b.real;
res.imag = b.imag + a.imag;
return res;
}
|
The module of a complex number is square root of the sum of the square
of the real and imag values.
Faites une fonction qui calcule le module d'un nombre complexe (la
racine de la somme du carr des deux composants).
Give a function that computes the module of a complexe number.
Donnez une fonction qui permet de comparer en grandeur deux nombres
complexes (on compare en fait leur module).
If we add this definition to bring a vector of complex numbers:
struct vecc {
int nbe;
complex tab [100];
};
typedef struct vecc vecc_t ;
this is a function to create such a vector:
Voici la fonction pour remplir un tel vecteur :
/* pour travailler les structures */
vecc_t remplirc (int nbc) {
int i;
vecc_t t;
float x, y;
t.nbe = nbc;
x = 4.0;
y = nbc / 10.0 + 0.1;
for (i = 0; i < nbc; i++) {
t.tab[i].real = x;
t.tab[i].imag = y;
x = x + 0.1;
y = y - 0.1;
}
return t;
}
void affic (vecc_t t) {
int i;
printf("Voici les %d nombres complexes\n", t.nbe);
for (i= 0; i < t.nbe; i++) {
printf("(%6.3f,%6.3f) ", t.tab[i].real, t.tab[i].imag);
}
printf("\n");
}
int main () {
vecc_t ta;
int n;
n = 10;
ta = remplirc(n);
affic (ta);
ta.tab[2] = addc(ta.tab[0],ta.tab[1]);
ta.tab[3] = multc(ta.tab[0],ta.tab[1]);
affic (ta);
}
|
it seems easy to answer these questions:
- La diffrence entre deux complexes.
- Soit un x, la somme des complexes du vecteur dont le module est suprieur x.
- Le second plus grand nombre complexe (utilisation du module, de mme que pour toute la suite),
- le troisime plus petit,
- le quatrime plus grand,
- ranger tout ce tableau dans l'ordre des modulos dcroissants en utilisant l'algorithme tri par insertion,
- ranger tout ce tableau dans l'ordre des modulos dcroissants en utilisant l'algorithme quicksort.
II.D.5) Unions
It's not a structure, but looks like one.
Nous devons traiter cette structure trs spciale.
/* pour s amuser avec des unions */
typedef unsigned short ushort;
typedef unsigned long ulong;
union etrange {
ushort sh;
ulong lg;
char c;
} ;
typedef union etrange strange_t;
void voir (strange_t s) {
printf("short %d\t long %d\t char %d\t car %c \n", s.sh, s.lg, (int) s.c, s.c);
}
int main () {
strange_t v;
v.lg = 1024;
voir (v);
v.lg = 1024 * 1024;
voir (v);
for (v.lg = 1; v.lg < 128; v.lg++)
voir (v);
}
/*
short 1024 long 1024 char 0 car
short 0 long 1048576 char 0 car
short 1 long 1 char 1 car
short 2 long 2 char 2 car
short 3 long 3 char 3 car
short 4 long 4 char 4 car
short 5 long 5 char 5 car
short 6 long 6 char 6 car
short 7 long 7 char 7 car
short 8 long 8 char 8 car
short 9 long 9 char 9 car
short 10 long 10 char 10 car
short 127 long 127 char 127 car
La suite, vous la verrez en faisant tourner le programme !
*/
|
Makefile
Compilation spare
Nous allons maintenant crer plusieurs fichiers et les compiler
sparment.
Le premier fichier contient les prototypes des fonctions. Il
s'agit du fichier "fac.h":
/* les prototypes des fonctions */
int fac (int);
int fac_acc (int, int);
void affiche (int, int);
|
Ensuite nous avons un fichier qui s'occupe des entres sorties, le
fichier "io.c":
#include "fac.h"
void affiche (int a, int b) {
printf("Vous avez donne \t%d\n",a);
printf("Sa factorielle est \t%d\n",b);
} |
Le fichier suivant contient la fonction du
calcul de la factorielle, c'est le fichier "fac.c":
#include "fac.h"
/* le calcul de la fonction factorielle */
int fac (int n) {
return fac_acc (n, 1);
}
int fac_acc (int n, int acc) {
if (n < 2) {
return acc;
}
else {
return fac_acc (n-1, n*acc);
}
} |
Enfin, le fichier "main.c" contient le reste du code (ici la
fonction main):
#include "fac.h"
main () {
int n, f;
n = 5;
f = fact(n);
affiche(n,f);
n = 6;
f = fact(n);
affiche(n,f);
} |
Il reste les compiler sparment. Ceci se gnralise grce au
fichier "Makefile":
# Compilation generique par Bourdin
CC=gcc
fac: io.o main.o fac.o fac.h
$(CC) io.o main.o fac.o -o fac
main.o: main.c fac.h
io.o: io.c fac.h
fac.o: fac.c fac.h
clean:
@rm -f *.o
@rm -f core
@rm -f *~
|
Attention, il faut remettre des "tabulations" la main, sous emacs.
Dans ce fichier on trouve trois sortes de lignes : les affectations de
variables (ici "CC=gcc") qui permettent d'utiliser des variables par
la suite, les dclarations de dpendance (comme "io.o: io.o fac.h",
qui annonce que la compilation de io.o dpend de l'existance des deux
autres fichiers) et les ordres (comme " @rm -f *.o" ou
" $(CC)
io.o main.o fac.o -o fac") qui sont des
lignes commenant par une tabulation.
Prenons la ligne 5:
fac est nomm "cible".
io.o main.o fac.o fac.h sont les dpendances.
Sous shell, il ne reste plus qu' demander la compilation
alpha5: make fac
predecessor cycle (io.o)
gcc -O -c io.c
predecessor cycle (main.o)
gcc -O -c main.c
predecessor cycle (fac.o)
gcc -O -c fac.c
gcc io.o main.o fac.o -o fac
ld: ERROR 33: Unresolved text symbol "fact" -- 1st referenced by main.o.
Use linker option -v to see when and which objects, archives and dsos are loaded.
ld: INFO 152: Output file removed because of error.
*** Error code 1 (bu21)
|
Aprs correction (la fonction est nomme "fac" et pas "fact"!):
alpha5: make fac
predecessor cycle (io.o)
predecessor cycle (main.o)
gcc -O -c main.c
predecessor cycle (fac.o)
gcc io.o main.o fac.o -o fac
alpha5: fac
Vous avez donne 5
Sa factorielle est 120
Vous avez donne 6
Sa factorielle est 720
alpha5: |
On peut amliorer ce fichier de make, en utilisant des variables et
des rgles :
# Meilleure compilation par Bourdin
#
# Attention, les tabulations doivent tre refaites vous-mmes, la
# main
#
OBJ=io.o main.o fac.o
CC=gcc
fac: $(OBJ) fac.h
$(CC) $(OBJ) -o fac
%.o : %.c
$(CC) -c $<
clean:
@rm -f *.o
@rm -f core
@rm -f *~
|
Vous remarquerez que les fichiers qui finissent par ".o" sont
obtenus par compilation avec l'option "-c" c'est l'objet des lignes
14 et 15.
Quelques variables par dfaut
- $@ dsigne le nom de la cible
- $< le nom de la premire dpendance
- $^ la liste des dpendances
- $? la liste des dpendances plus rcentes que la cible
- $* le nom du fichier sans suffixe
Voici les fichiers pour mettre en place l'algorithme de Newton,
tlcharger.
faire
- Reprendre un exemple prcdent, par exemple les chemins et
dnivels, et le sparer en plusieurs parties.
- Mettre toutes les parties dans un rpertoire correspondant.
- Fabriquer le fichier makefile correpondant.
- Faire tourner le programme.
A variable is a set of three things: a name, a type and a
location.
It is in this location that one can find the value of
the variable. The address is known by the operator &.
Une variable est un triplet < nom, type,
emplacement>. C'est cet emplacement
que, selon le type, on trouve la valeur.
On peut connatre l'emplacement, l'adresse, de la variable "a" en
utilisant l'oprateur & :
void voirou1 () {
int i, j;
printf("i est en %u, j est en %u\n", (int)&i, (int)&j);
}
|
One may also set this adress into a new variable, a "pointer". The
content of such a variable is available, and the content of the
pointed variable can be found with the unary operator *.
On peut aussi mettre cette adresse dans une variable spciale qui
contient des adresses, un pointeur. On peut aussi savoir ce
qu'il y a une certaine adresse avec l'oprateur unaire *.
/* une petite question sur les allocations */
#include <stdio.h>
void nrut (int * px, int * py) {
* px = * px + * py;
* py = * px - * py;
* px = * px - * py;
}
void lookatit (int n) {
int i, j, k, l;
int * pi, * pj;
i = 2;
j = 3;
k = 4;
l = 5;
pi = & i;
pj = & j;
printf("adresses de i %d et j %d\n",pi, pj);
printf("adresses de i %p et j %p\n",pi, pj);
nrut(pi,pj);
printf("valeurs de i %d et j %d\n",i, j);
pi = & k;
pj = & l;
printf("adresses contenues dans pi %d et pj %d\n",pi, pj);
printf("adresses contenues dans pi %p et pj %p\n",pi, pj);
}
int main () {
lookatit(5);
}
/*
adresses de i -317351240 et j -317351244
adresses de i 0x7ffeed159ab8 et j 0x7ffeed159ab4
valeurs de i 3 et j 2
adresses contenues dans pi -317351248 et pj -317351252
adresses contenues dans pi 0x7ffeed159ab0 et pj 0x7ffeed159aac
*/
|
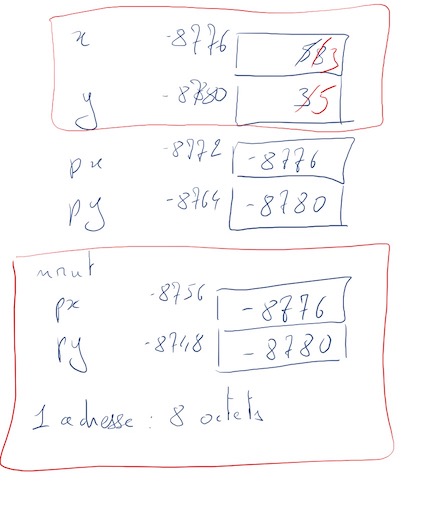 |
void voirou () {
int *pi, *pj;
int i, j;
printf("i est en %d, j est en %u\n",(int) &i,(int) &j);
pi = & i;
pj = & j;
i = 7;
j = 9;
printf("En %u il y a %d\n", (int) pi, * pi);
printf("En %u il y a %d\n", (int) &j, j);
}
|
On peut se servir des adresses pour modifier le contenu d'une variable
extrieure.
void iv (int * pa, int * pb) {
* pa = * pa + * pb;
* pb = * pa - * pb;
* pa = * pa - * pb;
}
int main () {
int a, v;
a = 5;
v = 8;
voirou1();
voirou();
printf("a = %d\t v = %d\n",a,v);
iv (&a, &v);
printf("a = %d\t v = %d\n",a,v);
}
/* dhcp13.ai.univ-paris8.fr: a.out
i est en 1344117452, j est en 1344117448
i est en 1344117436, j est en 1344117432
En 1344117436 il y a 7
En 1344117432 il y a 9
a = 5 v = 8
a = 8 v = 5
*/
|
Amusant, non ?
Voici un autre exemple, que vous reconnatrez aisment :
/* Fait par JJ B en 2010 */
typedef int * pint;
void fct (int nb, int rg, pint a, pint b) {
if (nb > rg) {
*a = *a + *b;
*b = *a - *b;
fct (nb, rg + 1, a, b);
}
}
main () {
int i, n, a, b;
n = 10;
for (i = 0; i <= n; i++) {
a = 1;
b = 1;
fct (i, 0, &a, &b);
printf("%d => %d\n", i, b);
}
}
|
- Retour
What is an array? Nothing else than a pointer.
Qu'est-ce qu'un tableau ? Un pointeur !
On peut parcourir un tableau, case case, par un pointeur :
/* Fait par JJ B en 2014 */
#include <stdio.h>
#include <stdlib.h>
struct vecteur {
int nbe;
float tab [100];
} ;
typedef struct vecteur vecteur_t;
typedef float * pfloat;
float somv (vecteur_t v) {
int i;
float som, *p;
p = v.tab;
som = 0;
for (i = 0; i < v.nbe; i++) {
som = som + *p;
p ++;
}
return som;
}
|
On suppose que le vecteur a t dfini par ailleurs. Voici une
illustration du fonctionnement de cette fonction :
Il vous reste reprendre quelques exercices faits avec des vecteurs,
mais cette fois, en utilisant les pointeurs.
Exemple avec les altitudes
#include <stdio.h>
typedef float table [100] [100];
void affichet (table t, int sx, int sy) {
int x, y;
printf("Tableau \n");
for (x = 0; x < sx; x += 1) {
for (y = 0; y < sy; y += 1) {
printf ("%3.3f ", t[x][y]);
}
printf("\n");
}
}
void afficheptr (table t, int sx, int sy) {
int x, y;
float * ptr;
printf("Tableau pointeurs\n");
for (x = 0; x < sx; x += 1) {
ptr = (float *) &(t[x]); /* mais pourquoi ? */
for (y = 0; y < sy; y += 1) {
printf ("%3.3f ", *ptr++);
}
printf("\n");
}
}
void afficheadr (table t, int sx, int sy) {
int x, y;
float * ptr;
printf("Adresses Tableau \n");
for (x = 0; x < sx; x += 1) {
ptr = (float *) &(t[x]);
for (y = 0; y < sy; y += 1) {
printf ("%d ", (int) ptr++ % 10000);
}
printf("\n");
}
}
void remplirt (table t, int sx, int sy) {
int x, y, sxy;
float v, eps, add;
v = 0.1;
add = 0.0;
sxy = sx * sx + sy * sy;
eps = 1.0 / (float) (sxy);
for (x = 0; x < sx; x += 1) {
for (y = 0; y < x; y += 1) {
t[x][y] = (float) (x * x - y * y + add) * eps;
}
for (y = x; y < sy; y += 1) {
t[x][y] = (float) ( y * y - x * x + add) * eps;
}
add += v;
if (add > 2.0)
v = - 0.1;
if (add < 0.1)
v = 0.1;
}
}
int main () {
table t;
int sizex, sizey;
sizex = 10;
sizey = 10;
remplirt(t, sizex, sizey);
affichet(t, sizex, sizey);
afficheptr(t, sizex, sizey);
afficheadr(t, sizex, sizey);
}
|
Qui donne l'excution :
0.000 0.005 0.020 0.045 0.080 0.125 0.180 0.245 0.320 0.405
0.005 0.001 0.015 0.041 0.075 0.120 0.175 0.240 0.315 0.400
0.021 0.016 0.001 0.026 0.061 0.106 0.161 0.226 0.301 0.386
0.047 0.041 0.026 0.002 0.036 0.081 0.136 0.201 0.276 0.361
0.082 0.077 0.062 0.037 0.002 0.047 0.102 0.167 0.242 0.327
0.127 0.122 0.107 0.082 0.047 0.002 0.057 0.122 0.197 0.282
0.183 0.178 0.163 0.138 0.103 0.058 0.003 0.068 0.143 0.228
0.249 0.243 0.228 0.204 0.169 0.124 0.068 0.004 0.078 0.163
0.324 0.319 0.304 0.279 0.244 0.199 0.144 0.079 0.004 0.089
0.410 0.405 0.389 0.364 0.329 0.285 0.229 0.164 0.089 0.005
Tableau pointeurs
0.000 0.005 0.020 0.045 0.080 0.125 0.180 0.245 0.320 0.405
0.005 0.001 0.015 0.041 0.075 0.120 0.175 0.240 0.315 0.400
0.021 0.016 0.001 0.026 0.061 0.106 0.161 0.226 0.301 0.386
0.047 0.041 0.026 0.002 0.036 0.081 0.136 0.201 0.276 0.361
0.082 0.077 0.062 0.037 0.002 0.047 0.102 0.167 0.242 0.327
0.127 0.122 0.107 0.082 0.047 0.002 0.057 0.122 0.197 0.282
0.183 0.178 0.163 0.138 0.103 0.058 0.003 0.068 0.143 0.228
0.249 0.243 0.228 0.204 0.169 0.124 0.068 0.004 0.078 0.163
0.324 0.319 0.304 0.279 0.244 0.199 0.144 0.079 0.004 0.089
0.410 0.405 0.389 0.364 0.329 0.285 0.229 0.164 0.089 0.005
Adresses Tableau
-7648 -7644 -7640 -7636 -7632 -7628 -7624 -7620 -7616 -7612
-7248 -7244 -7240 -7236 -7232 -7228 -7224 -7220 -7216 -7212
-6848 -6844 -6840 -6836 -6832 -6828 -6824 -6820 -6816 -6812
-6448 -6444 -6440 -6436 -6432 -6428 -6424 -6420 -6416 -6412
-6048 -6044 -6040 -6036 -6032 -6028 -6024 -6020 -6016 -6012
-5648 -5644 -5640 -5636 -5632 -5628 -5624 -5620 -5616 -5612
-5248 -5244 -5240 -5236 -5232 -5228 -5224 -5220 -5216 -5212
-4848 -4844 -4840 -4836 -4832 -4828 -4824 -4820 -4816 -4812
-4448 -4444 -4440 -4436 -4432 -4428 -4424 -4420 -4416 -4412
-4048 -4044 -4040 -4036 -4032 -4028 -4024 -4020 -4016 -4012
|
Le "pourquoi" vient simplement du fait que, lorsque le tableau est
cr, il contient 100x100 entiers. Donc, pour passer la ligne
suivante, il faudrait avancer de 400 octets...
- Dynamic arrays
Tableaux dynamiques
We oversize our arrays, is it such a good idea?
Jusqu' prsent, vous avez un problme avec la taille des tableaux et
vecteurs, ce n'est plus la peine grce aux tableaux dynamiques.
typedef int * pint;
typedef int table [100];
void fcttab (int nb, table t) {
int i;
pint p1, p2, p3;
p3 = t;
p2 = t + 1;
p1 = t + 2;
*p3 = 1;
*p2 = 1;
for (i = 2; i <= nb; i+=1) {
*p1 = *p2 + *p3;
p3 = p2;
p2 = p1;
p1+= 1;
}
}
void seetab (table t, int nb) {
pint p;
p = t;
while (nb > 0) {
printf("%d\t", *p);
p++;
nb--;
}
printf("\n");
}
main () {
table tt;
pint pt;
int n, nbele;
n = 18;
nbele = n + 1;
/* ici, la methode classique ou tt est un tableau */
fcttab(n, tt);
seetab(tt, nbele);
n = 10;
nbele = n + 1;
/* la, la methode dynamique de "creation" d'un tableau */
pt = (pint) malloc ((size_t) (nbele * sizeof(int)));
fcttab(n, pt);
seetab(pt, nbele);
free(pt);
/* c'est plus joli, plus souple, plus dynamique */
}
|
- Exercices
Refaire toutes les fonctions dj vues sur les tableaux mais avec des tableaux dynamiques.
Voici un exemple de corrig, l'ensemble du programme qui cre un
tableau d'altitudes (la topographie d'un terrain) et l'affiche (on
trouve le mme, " l'ancienne" un peu plus haut sur cette
page).
Let's see some new types to work on the altitude field.
Crons d'abord les types qui vont nous servir :
typedef unsigned int uint;
typedef float * tabalt ;
struct tableau {
tabalt t;
unsigned int nbc;
unsigned int nbl;
} ;
typedef struct tableau tableau;
|
This type includes the length in columns and lines of the array and
the adress of the values.
Comme vous le voyez, la structure tableau contient maintenant aussi
ses dimensions. On peut maintenant crer un tel tableau :
tableau creetableau (uint nbc, uint nbl) {
tableau t;
t.nbc = nbc;
t.nbl = nbl;
t.t = (tabalt) malloc ((size_t) (nbc * nbl * sizeof(float)));
return t;
}
|
Once it's created, it is easy to fill the array with values.
Une fois qu'il sera cr, on peut mettre une valeur dans une des
cases, ou rcuprer le contenu de l'une des cases :
void puttab (tableau t, uint i, uint j, float amettre) {
if (i < t.nbc && j < t.nbl) {
*(t.t + i + j * t.nbc) = amettre;
}
}
float valtab (tableau t, uint i, uint j) {
if (i < t.nbc && j < t.nbl) {
return *(t.t + i + j * t.nbc);
}
return -1.0;
}
|
Il ne reste plus qu' remplir systmatiquement le tableau avec les
mmes valeurs que dans l'exemple donn prcdemment :
void remplirtab (tableau t) {
uint i, j;
float val;
for (i = 0; i < t.nbc; i++)
for (j = 0; j < t.nbl; j++) {
val = (float) (30 * i + 20 * i * j + 15 * j);
while (val > 2000.0)
val = val - 2000.0;
if (val > 1000.0)
val = 2000.0 - val;
puttab(t, i, j, val);
}
}
|
Puis tre en mesure d'afficher toutes les cases du tableau :
void voirtab (tableau t) {
uint i, j;
for (j = 0; j < t.nbl; j++) {
printf ("%6d", j);
}
printf("\n");
for (i = 0; i < t.nbc; i++) {
printf ("%4d |", i);
for (j = 0; j < t.nbl; j++) {
printf ("%6.2f ", valtab(t, i, j));
}
printf("\n");
}
}
|
Une fonction main pour faire fonctionner tout cela et le tour
est jou.
int main () {
uint sx, sy;
tableau t;
sx = 10;
sy = 10;
t = creetableau (sx, sy);
remplirtab (t);
voirtab(t);
}
|
Voici un jeu d'essais :
0 1 2 3 4 5 6 7 8 9
0 | 0.00 15.00 30.00 45.00 60.00 75.00 90.00 105.00 120.00 135.00
1 | 30.00 65.00 100.00 135.00 170.00 205.00 240.00 275.00 310.00 345.00
2 | 60.00 115.00 170.00 225.00 280.00 335.00 390.00 445.00 500.00 555.00
3 | 90.00 165.00 240.00 315.00 390.00 465.00 540.00 615.00 690.00 765.00
4 |120.00 215.00 310.00 405.00 500.00 595.00 690.00 785.00 880.00 975.00
5 |150.00 265.00 380.00 495.00 610.00 725.00 840.00 955.00 930.00 815.00
6 |180.00 315.00 450.00 585.00 720.00 855.00 990.00 875.00 740.00 605.00
7 |210.00 365.00 520.00 675.00 830.00 985.00 860.00 705.00 550.00 395.00
8 |240.00 415.00 590.00 765.00 940.00 885.00 710.00 535.00 360.00 185.00
9 |270.00 465.00 660.00 855.00 950.00 755.00 560.00 365.00 170.00 25.00
|
Avec ce tableau, il faut faire quelques fonctions.
- pour deux points voisins, (i1,j1) et (i2,j2) donner le dnivel
entre les deux.
- pour deux points de la mme horizontale, donner la somme des
dnivels positifs entre eux.
- pour deux points de la mme verticale, donner la somme des
dnivels positifs entre eux.
- pour deux points de la mme verticale, donner la somme des
dnivels positifs et la somme des dnivels ngatifs entre
eux. (utilisation d'une structure ad hoc).
- pour deux points donns, calculer les dnivels positifs et
ngatifs entre eux, selon la droite qui les joint.
- Lisp like lists
Liste Lisp
Voici une fonction qui construit une liste de n nombres
entiers. Elle est en Lisp, il faut donc la transcrire.
(define (creerl n)
(if (< n 1)
'(0)
(cons n (creerl (- n 1)))))
|
- Type definition
Dfinition des types
struct cell {
int nb;
struct cell * nxt;
} ;
typedef struct cell cell_t;
typedef struct cell * liste;
|
O on voit que la liste est en fait uniquement l'adresse d'une
structure qui contient une valeur et une liste.
- fonctions simples
int estvide (liste l) {
if (l == (liste) 0) {
return 1;
}
return 0;
}
int estnonvide (liste l) {
if (l == (liste) 0) {
return 0;
}
return 1;
}
|
- La somme des lments
int soml (liste l) {
if (estvide(l)) {
return 0;
}
return (*l).nb + soml((*l).nxt);
}
|
- Le nombre d'lments
int howmany (liste l) {
if (estvide(l)) {
return 0;
}
return 1 + howmany ((*l).nxt);
}
|
- La construction
liste cons (int nb, liste l) {
liste new;
new = (liste) malloc (sizeof(cell_t));
assert(new);
(*new).nb = nb;
(*new).nxt = l;
return new;
}
liste creer (int nb) {
liste debut;
int i, j, k, t;
j = 13;
k = 21;
debut = (liste) 0;
for (i = 0; i < nb; i++) {
debut = cons (j, debut);
t = (j + k) % 33;
k = j;
j = t;
}
return debut;
}
|
- Trois fonctions d'affichage
void affl (liste l) {
if (estvide (l)) {
printf("\n");
}
else {
printf("%3d ", (*l).nb);
affl ((*l).nxt);
}
}
|
void affll (liste l) {
if (estvide (l)) {
printf("\n");
}
else {
printf("%3d ", l->nb);
affll (l->nxt);
}
}
void affw (liste l) {
while (estnonvide (l)) {
printf("%3d ", l->nb);
l = l->nxt;
}
printf("\n");
}
|
Des enttes inclure :
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
|
La fonction main :
int main () {
liste l;
int nb, s;
nb = 10;
l = creer(nb);
affw(l);
s = soml(l);
printf("Total : %d\n", s);
s = howmany(l);
printf("Il y a %d elements\n", s);
}
|
- Liste d'exercices faire.
- Trouver le plus grand lment.
- Afficher les lments dans l'ordre inverse.
- Mettre les lments de la liste en ordre
inverse. (Attention, il n'y a pas besoin de malloc pour faire
cette fonction).
- Fabriquer une liste avec les n premiers entiers (dans l'ordre dcroissant).
- Faire la somme des lments d'une liste.
- Faire la somme des lments plus petits que 50 d'une liste.
- Faire la moyenne des lments d'une liste.
- Enlever le premier lment d'une liste.
- Enlever le dernier lment d'une liste.
- Fonction de concatnation de deux listes.
- Dans une liste range, insrer une cellule sa place.
- Faire le tri d'une liste, par insertion.
- Trouver le mdian des lments d'une liste.
- Fabriquer une liste des carrs de tous les lments d'une
autre liste passe en paramtre.
Exemple de solution
int plusgrandliste (liste l, int candidat) {
if (l) {
if (l->nb > candidat)
return plusgrandliste (l->next, l->nb);
return plusgrandliste (l->next, candidat);
}
return candidat; /* il n'y a plus d'autre possible*/
}
int plusgrandl (liste l) {
if (l)
return plusgrandliste (l->next, l->nb);
return INT_MIN; /* impose d'avoir inclus limits.h */
}
|
- Quicksort sur une liste
Pour faire Quicksort, nous avons besoin de faire une fonction
qui trie les toutes petites listes.
liste tril2(liste l) {
liste crt ;
if (!l)
return l;
if (! l->nxt)
return l;
crt = l->nxt;
if (l->nb < crt->nb)
return l;
crt->nxt = l;
l->nxt = NULL;
return crt;
}
|
Il ne reste plus qu' faire quicksort :
- sparer la liste en trois
parties, le pivot, les petits et les grands,
- utiliser qs pour ranger les petits,
- utiliser qs pour ranger les grands,
- remettre bout bout les trois ensembles.
liste qs (liste l) {
liste petits, grands, pivot, crt;
if (!l)
return l;
if (! l->nxt)
return l;
if (! l->nxt->nxt)
return tril2(l);
pivot = l;
l = l->nxt;
pivot->nxt = NULL;
petits = NULL;
grands = NULL;
while (l) {
crt = l->nxt;
if (l->nb < pivot->nb) {
/* il est petit */
l->nxt = petits;
petits = l;
}
else {
/* il est grand */
l->nxt = grands;
grands = l;
}
l = crt;
}
grands = qs(grands);
petits = qs(petits);
pivot->nxt = grands;
if (! petits)
return pivot;
crt = petits;
while (crt->nxt)
crt = crt->nxt;
crt->nxt = pivot;
return petits;
}
|
- Inversion d'une liste.
- Inversion par la mthode PG/DG.
(define (re l)
(ifn (cdr l) l
(cons (car (re (cdr l)))
(re (cons (car l)
(re (cdr (re (cdr l)))))))))
|
Quelques solutions vues en cours
- Moyenne des lments de la liste
C'est pourtant simple : d'une part on compte le nombre d'lments
d'autre part on fait la somme des lments. Ensuite on divise.
Attention, il faut traiter, au dbut, le cas o la liste est vide.
int moyl (liste l) {
int val, nb;
liste crt;
if (! l)
return 0;
val = 0;
nb = 0;
crt = l;
while (crt) {
val += car(crt);
crt = cdr(crt);
nb++;
}
return val/nb;
}
|
- Cration d'une liste de nombres dcroissants
"La beaut des arbres est de crotre." (qui ?)
Nous prsentons une structure pour des arbres binaires.
We start by defining some structures.
/* Arbres binaires tout simplement */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
struct noeud {
int num;
float val;
struct noeud * fg;
struct noeud * fd;
} ;
typedef struct noeud noeud;
typedef struct noeud * arbre;
|
We'll add a new set of values in the tree.
arbre ajout (arbre a, int v, float x) {
arbre new;
int rande;
if (! a) {
new = (arbre) malloc (sizeof (noeud));
new->num = v;
new->val = x;
new->fg = (arbre) 0;
new->fd = (arbre) 0;
return new;
}
rande = rand ();
/*
printf(" insere %d en %d avec %2d\n", v, a->num, rande %10);
*/
if (rande % 2) {
/* on le met gauche*/
if (! (a->fg)) {
/* s'il ny a pas de fils gauche */
a->fg = (arbre) malloc (sizeof (noeud));
a->fg->num = v;
a->fg->val = x;
a->fg->fg = (arbre) 0;
a->fg->fd = (arbre) 0;
return a;
}
a->fg = ajout(a->fg, v, x);
return a;
}
/* on le met donc a droite*/
if (! (a->fd)) {
/* s'il ny a pas de fils droit */
a->fd = (arbre) malloc (sizeof (noeud));
a->fd->num = v;
a->fd->val = x;
a->fd->fg = (arbre) 0;
a->fd->fd = (arbre) 0;
return a;
}
a->fd = ajout(a->fd, v, x);
return a;
}
/*
To create the tree, you add, one after the other, the values in the
tree.*/
arbre creation (int n) {
arbre a;
float x, y;
x = 1.5;
y = 0.21;
a = (arbre) 0;
srand(time(NULL));
while (n--) {
a = ajout (a, n, x);
printf("\n");
x += y;
y += 0.06;
if (x > 3.0 || x < -2.0) {
y = - y;
}
}
return a;
}
|
It is also possible to show the tree created:
void afficharbre (arbre a) {
if (a) {
afficharbre (a->fg);
printf("%d %3.2f ", a->num, a->val);
afficharbre (a->fd);
}
}
|
int appartient (int nu, arbre a) {
if (! a)
return 0;
if (a->num == nu)
return 1;
if (appartient (nu, a->fd))
return 1;
return appartient (nu, a->fg);
}
|
Vous pouvez aussi :
- Trouver le plus grand val dans un arbre.
- Trouver le second plus petit val dans un arbre.
- Compter le nombre de noeuds de l'arbre.
- Compter le nombre de noeuds dont le champ val est
suprieur une valeur donne.
- Compter le nombre de feuilles de l'arbre (une feuille est
un noeud qui n'a aucun successeur).
- Renvoyer la profondeur d'un noeud de l'arbre.
La profondeur est le nombre de gnrations entre la racine
de l'arbre et la cellule cherche. La racine
est la profondeur 0, ses successeurs directs la profondeur
1, etc.
- Renvoyer la profondeur maximale de l'arbre.
int main () {
int n;
arbre a, b;
float x;
/*
srand(time(NULL));
*/
n = 20;
a = creation (n);
printf("\n Vois \n");
voisarbre (a,0);
x = 0.72;
printf("%f dedans %s\n", x, appartient(a,x) ? "Oui" : "Non");
}
|
Oh, il ne le trouve pas :
Il faut donc faire une approximation :
int fappartient (arbre a, float x) {
if (! a)
return 0;
if (fabs(a->val - x) < 0.0001)
return 1;
return fappartient(a->fg, x) || fappartient (a->fd, x);
}
|
int main () {
int n;
arbre a, b;
float x;
/*
srand(time(NULL));
*/
n = 20;
a = creation (n);
printf("\n Vois \n");
voisarbre (a,0);
x = 0.72;
printf("%f dedans %s\n", x, appartient(a,x) ? "Oui" : "Non");
printf("%f dedans %s\n", x, fappartient(a,x) ? "OUI" : "NON");
}
|
Cette fois :
0.720000 dedans Non
0.720000 dedans OUI
|
Arbres binaires de recherche
Binary search tree
The structure is the same but two conditions are respected:
for a node with value n, every value in its left part are lower than
n
and every value in its right part are greater or equal than n.
Here after is a function that build a BST.
C'est la mme structure mais elle respecte deux conditions : pour
tout sommet de valeur n, tous
ses descendants gauche ont une valeur infrieure n et tous ses
descendants droite one une valeur suprieure ou gale n.
Hereafter is the adequate construct function:
arbre ajout (arbre a, int v, float x) {
arbre new;
if (! a) {
new = (arbre) malloc (sizeof (noeud));
new->num = v;
new->val = x;
new->fg = (arbre) 0;
new->fd = (arbre) 0;
return new;
}
if (x < a->val) {
/* on le met gauche*/
if (! (a->fg)) {
/* s'il ny a pas de fils gauche */
a->fg = (arbre) malloc (sizeof (noeud));
a->fg->num = v;
a->fg->val = x;
a->fg->fg = (arbre) 0;
a->fg->fd = (arbre) 0;
return a;
}
a->fg = ajout(a->fg, v, x);
return a;
}
/* on le met donc a droite*/
if (! (a->fd)) {
/* s'il ny a pas de fils droit */
a->fd = (arbre) malloc (sizeof (noeud));
a->fd->num = v;
a->fd->val = x;
a->fd->fg = (arbre) 0;
a->fd->fd = (arbre) 0;
return a;
}
a->fd = ajout(a->fd, v, x);
return a;
}
arbre creation (int n) {
arbre a;
float x, y;
x = 1.5;
y = 0.21;
a = (arbre) 0;
while (n--) {
a = ajout (a, n, x);
x += y;
y += 0.06;
if (x > 3.0 || x < -2.0) {
y = - y;
}
}
return a;
}
|
Il vous reste faire la nouvelle fonction d'appartenance d'une valeur
( virgule) dans cet arbre.
int appartient (arbre a, float x) {
if (! a)
return 0;
if (a->val == x)
return 1;
if (a->val > x)
return appartient (a->sg, x);
return appartient (a->sd, x);
}
int appartientf (arbre a, float x) {
if (! a)
return 0;
if (fabsf(a->val - x) < 0.0001)
return 1;
if (a->val > x)
return appartientf (a->sg, x);
return appartientf (a->sd, x);
}
|
Puis une fonction qui compte le nombre d'occurences d'une valeur
virgule dans cet arbre.
Puis une fonction qui affiche toutes les valeurs (val) dans l'ordre croissant.
Puis une fonction qui affiche toutes les valeurs (val) dans l'ordre dcroissant.
Puis une fonction qui renvoie le nombre de sommets de l'arbre.
IV.A) Compiler
Rgles de Compilation
- The four steps for compiling
Les quatre tapes de la compilation
- The preprocessor. La prcompilation (on obtient le rsultat en utilisant
l'option -E)
- Assembly code. le code assembleur (option -S)
- Building of the object code. le code objet (option -c)
- The linker. l'dition de liens (option -o et le nom de l'excutable).
- The preprocessor
It obeys to orders starting with #. Examples:
Les directives qui commencent par # et elles seules sont vallues par
le prcompilateur. Il les excute. Parmi ces directives nous verrons
essentiellement les :
- #define
- #include
- #if then else
Pseudo-constants and pseudo-functions
pseudo-constantes et pseudo-fonctions
Il s'agit de remplacer dans le texte, dans le corps du programme,
toute occurence du mot dfini par sa dfinition. Exemple :
#define MAXI 100
every occurence of MAXI will be replaced by 100.
#include <stdio.h>
#define GT(a, b) a < b ? b : a
#define CARRE(a) a * a
main () {
int i, s;
i = 10;
s = 12;
printf("Le MAX de %3d et %3D est %d\n",i,s,GT(i,s));
printf("Le MAX de %3d et %3D est %d\n",i,s, GT(i++,s++));
printf("Le MAX de %3d et %3D est %d\n",i,s, GT(i+1,s+1));
printf("Le carre de %3d est %d\n",i + 1,CARRE(i + 1));
printf("Le carre de %3d est %d\n",i,CARRE(i++));
printf("Le carre de %3d est %d\n",i,CARRE(--i));
}
|
After preprocessoring, this part of the program becomes:
aprs
compilation partielle, devient
main () {
int i, s;
i = 10;
s = 12;
printf("Le MAX de %3d et %3D est %d\n",i,s,i < s ? s : i);
printf("Le MAX de %3d et %3D est %d\n",i,s, i++ < s++ ? s++ : i++);
printf("Le MAX de %3d et %3D est %d\n",i,s, i+1 < s+1 ? s+1 : i+1);
printf("Le carre de %3d est %d\n",i + 1,i + 1 * i + 1);
printf("Le carre de %3d est %d\n",i,i++ * i++);
printf("Le carre de %3d est %d\n",i,--i * --i);
}
|
The program does:
dhcp2.ai.univ-paris8.fr: a.out
Le MAX de 10 et 12 est 12
Le MAX de 10 et 12 est 13
Le MAX de 11 et 14 est 15
Le carre de 12 est 23
Le carre de 11 est 132
Le carre de 13 est 132
|
Et que diriez-vous de ce rsultat paradoxal ?
#define MAX(s,t) s < t ? t : s
main () {
int i, j, k, m, n;
i = 2;
j = 5;
k = 6;
n = MAX(i,j);
m = MAX(n, k);
printf("MAX(%3d,%3d,%3d) == %3d\n",i,j, k, m);
printf("MAX(%3d,%3d,%3d) == %3d\n",i,j, k, MAX(MAX(i,j),k));
}
|
a a l'air tout simple et, presque, normal, non ? Essayons.
jj@mu $ a.out
MAX( 2, 5, 6) == 6
MAX( 2, 5, 6) == 5
jj@mu $
|
... qui n'est pas tout fait normal.
Let's look at the preprocessed code:
jj@mu $ gcc -E ex.c
# 1 "ex.c"
# 1 ""
# 1 ""
# 1 "ex.c"
main () {
int i, j, k, m, n;
i = 2;
j = 5;
k = 6;
n = i < j ? j : i;
m = n < k ? k : n;
printf("MAX(%3d,%3d,%3d) == %3d\n",i,j, k, m);
printf("MAX(%3d,%3d,%3d) == %3d\n",i,j, k, i < j ? j : i < k ? k : i < j ? j : i);
}
|
Just look at it and the error seems ovious.
Cette fois je vois bien o est l'erreur, dans ce cas on regarde, si i
est plus petit que j on revoie j, sinon on fait l'valuation de i plus
petit que k. C'est idiot, on voudrait justement le contraire !
- Libraries
Bibliothques
There are some very well documented standard libraries, you should
check them on:
On trouvera de la documentation prcise sur les bibliothques standard sur
le lien suivant. Vous devriez en prendre connaissance.
- Dcalages
Remarquons :
Dcimal Binaire
3 11
6 110
12 1100
24 11000
48 110000
96 1100000
192 11000000
4 100
8 1000
16 10000
13 1101
26 11010
Remarquons que, en dcimal, 1230 et dix fois plus grand que 123. Donc,
en binaire, 101010 et deux fois plus grand que 10101. L'oprateur de
dcalage gauche <<
permet donc de dcaler un nombre binaire de n
cases donc de le multiplier par 2 puissance n.
void puiss2 (int pmax) {
int i, p;
p = 1;
for (i=0; i < pmax; i++) {
printf("%d\t",p);
p = p << 1;
}
printf("\n");
}
|
Bien sr le dcalage droite fait exactement le contraire.
Attention, pour les nombres ngatifs, comme vous le savez, pour que le
nombre reste ngatif, si le premier chiffre est un 1, au cours du
dclage droite, ce sont des 1 qui sont mis gauche !
- Et binaire
01011010
& 00011100
------------
00011000
01011010
& 00000001
------------
00000000
S'crit avec &.
int imper (int i) {
return i & 0x01;
}
|
- Ou binaire
int nonul (int i) {
while (i) {
if (i | 0x01)
return 1;
i = i << 1;
}
return 0;
}
/* completement inutile, non */
|
- Ou bien binaire
int differ (int i, int j) {
if (i ^ j)
return 1;
return 0;
}
|
- Non binaire
Essayez donc ceci :
int inver (int i) {
return 1 + ~i;
}
int main () {
int n;
for (n = -10; n < 11; n++)
printf("%d == - %d\n", n, inver(n));
}
|
- First example see in class on March the 25th 2020
To write on a file one needs to open it and... to write on it.
We start by the vector definition.
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
struct vect {
int nbele;
int * v;
} ;
typedef struct vect vect_t;
|
Print such a vector is easy :
void afficv(vect_t v) {
int i;
for (i = 0; i < v.nbele; i++)
printf("%d ",v.v[i]);
printf("\n");
}
|
Read from a file, first the number of elements then the elements is
easy too, as soon as we have a file descriptor :
vect_t lire (FILE * fd, int nbele) {
vect_t v;
int i, nbelefic, tmp;
v.nbele = nbele;
fscanf(fd, "%d ", &nbelefic);
if (nbelefic < nbele) {
nbele = nbelefic;
}
v.v = (int *) malloc (nbele* sizeof(int));
assert(v.v);
for(i=0; i < nbele; i++) {
fscanf(fd, "%d", &tmp);
v.v[i] = tmp;
}
return v;
}
|
Write such a file should not worry you :
void ecrire (FILE * fd, vect_t w) {
int i;
fprintf(fd,"%9d ",w.nbele);
printf(" on met %d\n",w.nbele);
for (i = 0; i < w.nbele; i++)
fprintf(fd,"%9d ",w.v[i]);
fprintf(fd,"\n");
}
|
All that remain are two simple functions.
vect_t creervect(nb) {
int i, a, b, c;
vect_t w;
w.nbele = nb;
w.v = (int *) malloc (nb * sizeof(int));
assert(w.v);
a = 1;
b = 1;
w.v[0]=1;
w.v[1]=1;
for (i = 2; i < nb; i++) {
c = a + b;
w.v[i] = c;
b = a;
a = c;
}
return w;
}
int main (int argc, char * * argv) {
int nb, lireou;
FILE * fd;
vect_t w;
if (argc != 3) {
printf(" Mode : a.out nb nmfic\rn nb est un entier et nmfic un nom de fichier\n");
exit (0);
}
nb = atoi (argv[1]);
printf("argv[1] valait %d\n", nb);
printf("Pour lire (1) ou ecrire (2) ?\n");
scanf("%d",&lireou);
if (lireou == 1) {
fd = fopen(argv[2],"r+");/* open the file to read it*/
assert(fd);
w = lire(fd,nb);
afficv(w);
printf("Ou suis-je ? %ld\n",ftell(fd));
fseek(fd, 0L, 0);
printf("Ou suis-je ? %ld\n",ftell(fd));
fseek(fd, -10L, SEEK_END);
printf("Ou suis-je ? %ld\n",ftell(fd));
fclose(fd);
exit (0);
}
printf("On va ecrire \n");
fd = fopen(argv[2],"w");/* open the file to write it*/
assert(fd);
w = creervect(nb);
afficv(w);
ecrire(fd,w);
fclose(fd);
exit (0);
}
/* r r+ w w+ a a+
O debut debut dbut dbut fin fin
non err err creation
ftell(fd) -> le numro de la case du fichier (0 c'est le dbut, 1 le second octet...)
fseed(fd,ecart,point) permet d'avancer de "ecart" octets partir du "point"
SEEK_SET 0
SEEK_CUR 1
SEEK_END 2
*/
|
- Second example
#include <stdio.h>
#include <stdlib.h>
struct vectd {
int nb;
double * v;
} ;
typedef struct vectd vectd_t;
|
Then we are able to write such a vector on the terminal:
void afficher (vectd_t v){
int i;
printf("%d ",v.nb);
for (i = 0; i < v.nb; i++)
printf("%lf ",v.v[i]);
printf("\n");
}
|
... or on the file:
void ecrire (vectd_t v, char * nomfichier) {
int i;
FILE * fd;
fd = fopen (nomfichier, "w");
if (! fd) { /* good old ways */
printf("Impossible d ouvrir le fichier %s !\n\n", nomfichier);
exit (1);
}
fprintf(fd,"%d ",v.nb);
for (i = 0; i < v.nb; i++)
fprintf(fd,"%lf ",v.v[i]);
fclose(fd);
}
|
we need to create it:
vectd_t creer (int nb) {
vectd_t v;
int i;
double x, eps;
v.nb = nb;
v.v = (double *) malloc (nb * sizeof(double));
if (! v.v) {
printf("Impossible d allouer la memoire de taille %d !\n\n", nb);
exit (1);
}
eps = - 0.07;
for (i = 0, x=1.3; i < v.nb; i++) {
v.v[i] = x;
x += eps;
if (x < 1.0)
eps = 0.145 + eps;
if (x > 1.7)
eps = - 0.145 + eps;
}
return v;
}
|
or to read it from the file:
vectd_t lire (char * nomfichier) {
vectd_t v;
int i, nb;
FILE * fd;
double x;
fd = fopen (nomfichier, "r");
if (! fd) {
printf("Impossible d ouvrir le fichier %s !\n\n", nomfichier);
exit (1);
}
fscanf(fd,"%d ",&nb);
v.nb = nb;
v.v = (double *) malloc (nb * sizeof(double));
if (! v.v) {
printf("Impossible d allouer la memoire de taille %d !\n\n", nb);
exit (1);
}
for (i = 0; i < v.nb; i++) {
fscanf(fd,"%lf ",&x);
v.v[i] = x;
}
fclose(fd);
return v;
}
|
Here is a main function to use all the functions above.
int main (int argc, char * * argv) {
int nb, choix;
vectd_t w;
char * nf = "donnees.txt";
choix = 0;
if (argc == 3) {
choix = atoi (argv[1]);
nb = atoi (argv[2]);
printf("creation du fichier avec %d valeurs\n", nb);
w = creer(nb);
afficher(w);
ecrire(w,nf);
return 0;
}
if (argc == 2) {
choix = atoi (argv[1]);
}
if (choix < 0 || choix > 1)
choix = 0;
switch(choix) {
case 0:
printf("creation du fichier\n");
nb = 21;
w = creer(nb);
afficher(w);
ecrire(w,nf);
break;
case 1:
printf("lecture du fichier\n");
w = lire(nf);
afficher(w);
break;
}
}
|
- Second example
We need to read and write files. Let's start with some definitions.
Nous allons voir maintenant comment on crit et comment on peut lire
les contenus de fichiers. D'abord, il nous faut quelques dfinitions,
c'est le fichier mydef.h :
- Third example
- A quicker version
Version plus rapide
The prototypes and definitions are given at first:
Nous donnons ici simplement les fichiers direct.h, qui contient les dcalrations et prototypes,
/* direct.h*/
#include <stdio.h>
#include <stdlib.h>
int fibiter (int);
int lire (FILE *, int);
int remplir (FILE *, int);
|
the file with the main function
puis le fichier contenant la fonction main
/* miam.c */
#include "direct.h"
#define NOM "fib.dat"
#define NORMAL 43
main (int argc, char * * argv) {
FILE * fichier;
int i, j, v, w;
if (argc == 2) {
i = atoi (argv [1]);
if ((fichier = fopen(NOM,"r+"))!= NULL) {
// printf("On cherche fib(%d)\n",i);
v = lire (fichier, i);
printf("fib(%d) = %d\n",i,v);
}
else {
if ((fichier = fopen(NOM,"w+"))== NULL) {
printf(" Rien a faire nous revenons a une fonction classique\n");
v = fibiter (i);
printf("fib(%d) = %d\n",i,v);
}
else {
v = remplir (fichier, i);
printf("fib(%d) = %d \n",i,v);
}
}
fclose(fichier);
}
else { /* Taille indefinie */
if ((fichier = fopen(NOM,"r+"))== NULL) {
printf("il faut creer ce fichier \n\n");
fichier = fopen(NOM,"w+");
v = remplir (fichier, NORMAL);
w = lire (fichier, NORMAL);
printf("fib(%d) = %d == %d\n",NORMAL,v, w);
fclose (fichier);
}
else {
v = lire (fichier, NORMAL);
printf("fib(%d) = %d \n",NORMAL,v);
close(fichier);
}
}
}
|
then the two functions of file direct.c
puis les deux fonctions qui composent le fichier direct.c, lire
/*direct.c*/
/* Il s agit de lire et d ecrire dans un fichier massif */
#include "direct.h"
int lire (FILE * f, int nb) {
int nf, i, v, w, * tf;
/* on commence par savoir s'il y a assez d'elements dans f*/
fread(&nf, (size_t) 4, (size_t) 1, f);
printf("Dans ce fichier il y a %d elements\n",nf);
if (nf > nb) {
tf = (int *) malloc ((nb+1) * sizeof (int));
fread(tf, (size_t) 4, (size_t) (1 + nb), f);
for (i=0; i <= nb; i++) {
printf("fib(%d) == %d\n",i, tf[i]);
}
return tf[nb];
}
else {
return remplir (f, nb);
}
}
|
then remplir(fill it)
puis remplir
int remplir (FILE * f, int nb) {
int nf, i, v, w, * tf;
tf = (int *) malloc ((nb+1) * sizeof (int));
tf[0] = 1;
tf[1] = 1;
for (i=2, v=1, w=1; i <= nb; i++) {
v += w;
tf[i] = v;
w = v - w;
}
for (i=0; i < nb; i++) {
printf("fib(%d) = %d\n",i,tf[i]);
}
fseek (f,0,SEEK_SET);
fwrite(&nb, (size_t) 4, (size_t) (1), f);
fwrite(tf, (size_t) 4, (size_t) (1 + nb), f);
return tf[nb];
}
|
All that is to do now is compile and run the program.
Il ne reste plus qu' copiler.
Vous pouvez utiliser LaTeX pour rdiger votre projet. Pour cela vous
trouverez ici plusieurs fichiers :
Dernire mise jour le 19/4/2021 14h00