Sven De Félice et Jean-Jacques BOURDIN
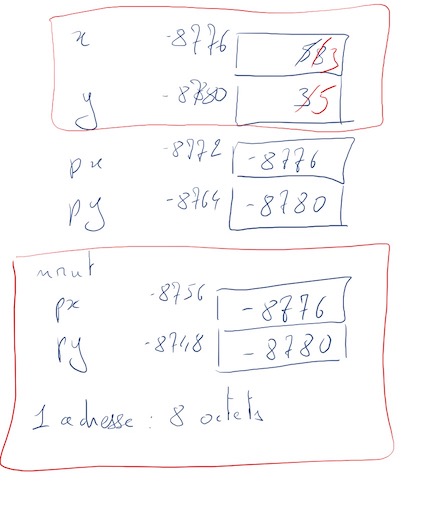
A variable is a set of three things: a name, a type and a
location.
It is in this location that one can find the value of
the variable. The address is known by the operator &.
Une variable est un triplet < nom, type, emplacement>. C'est à cet emplacement que, selon le type, on trouve la valeur. On peut connaître l'emplacement, l'adresse, de la variable "a" en utilisant l'opérateur & :
void voirou1 () {
int i, j;
printf("i est en %u, j est en %u\n", (int)&i, (int)&j);
}
|
void voirou () {
int *pi, *pj;
int i, j;
printf("i est en %d, j est en %u\n",(int) &i,(int) &j);
pi = & i;
pj = & j;
i = 7;
j = 9;
printf("En %u il y a %d\n", (int) pi, * pi);
printf("En %u il y a %d\n", (int) &j, j);
}
|
void iv (int * pa, int * pb) {
* pa = * pa + * pb;
* pb = * pa - * pb;
* pa = * pa - * pb;
}
int main () {
int a, v;
a = 5;
v = 8;
voirou1();
voirou();
printf("a = %d\t v = %d\n",a,v);
iv (&a, &v);
printf("a = %d\t v = %d\n",a,v);
}
/* dhcp13.ai.univ-paris8.fr: a.out
a = 5 v = 8
a = 8 v = 5
*/
|
nom adresse contenus
main a 400 5 puis 13 puis 8
main v 404 8 puis 5
iv pa 408 400
iv pb 416 404
Amusant, non ?
/* une autre version */
#include <stdio.h>
void nrut (int * px, int * py) {
* px = * px + * py;
* py = * px - * py;
* px = * px - * py;
}
void lookatit (int n) {
int x, y;
int * px, * py; /* adresses de int */
x = n;
y = 3;
px = & x;
py = & y;
printf("adresses de x %p et y %p\n",px, py);
printf("Avant : valeurs de x %d et y %d\n",x, y);
nrut(px,py);
printf("Avant : valeurs de x %d et y %d\n",x, y);
}
int main () {
lookatit(5);
}
/*
adresses de x 0x7ff7b32b7768 et y 0x7ff7b32b7764
Avant : valeurs de x 5 et y 3
Apres : valeurs de x 3 et y 5
*/
|
 |
/* Fait par JJ B en 2010 */
typedef int * pint;
void fct (int nb, int rg, pint a, pint b) {
if (nb > rg) {
*a = *a + *b;
*b = *a - *b;
fct (nb, rg + 1, a, b);
}
}
main () {
int i, n, a, b;
n = 10;
for (i = 0; i <= n; i++) {
a = 1;
b = 1;
fct (i, 0, &a, &b);
printf("%d => %d\n", i, b);
}
}
|
/* Fait par JJ B */
#include <stdio.h>
#include <stdlib.h>
struct vecteur {
int nbe;
float tab [100];
} ;
typedef struct vecteur vecteur_t;
typedef float * pfloat;
float somv (vecteur_t v) {
int i;
float som;
pfloat p;
p = v.tab;
som = 0;
for (i = 0; i < v.nbe; i++) {
som = som + *p;
p ++;
}
return som;
}
|
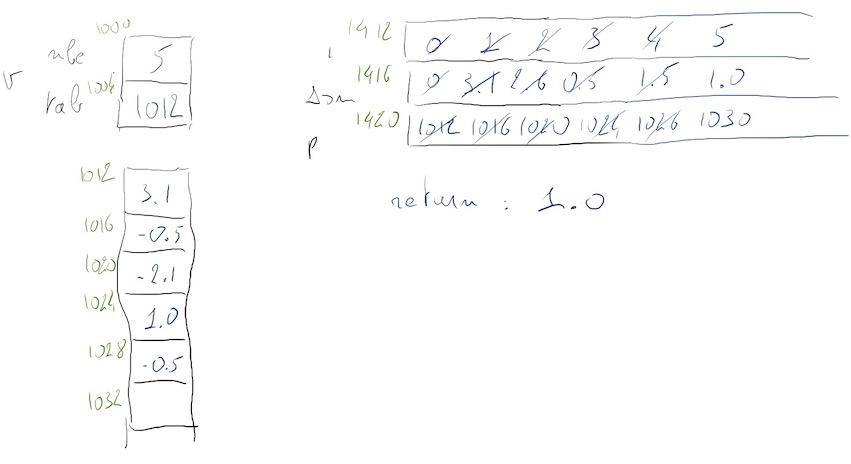 |
Il vous reste à reprendre quelques exercices faits avec des vecteurs, mais cette fois, en utilisant les pointeurs.
Exemple avec un vecteur de nombre complexes
Nous complétons la structure de nombres complexes vues dans le TP. Ceci serait bien placé dans un fichier Header.
#include <stdio.h>
#include <stdlib.h>
struct compl {
float r; // représente la partie réelle
float i; // représente la partie imaginaire
} ;
typedef struct compl compl_t;
struct vecc {
int nbc;
compl_t vc [100];
float vm [100]; /* le module pour chacun */
} ;
typedef struct vecc vecc_t;
vecc_t creevec (int);
vecc_t calculmodule (vecc_t);
void affvec (vecc_t);
int mini (vecc_t);
|
Les autres fonctions sont à écrire par vous-mêmes.
#include "comp.h"
int main () {
vecc_t v, w;
int n, i;
float mod, modmoy;
n = 20;
v = creevec(n);
printf("Avant le module \n");
affvec (v);
v = calculmodule(v);
printf("Avant le module \n");
affvec (v);
i = mini (v);
printf("le plus petit est le numéro %2d \t %f i%f et son module %f\n", i, v.vc[i].r, v.vc[i].i, v.vm[i]);
}
vecc_t creevec (int nb) {
float reel, imag, eps;
int i;
vecc_t v;
v.nbc = nb;
reel = 1.0;
imag = 2.0;
eps = 0.13;
for (i = 0; i < nb; i++) {
v.vc[i].r = reel;
v.vc[i].i = imag;
reel += eps;
imag -= eps;
if (reel > 2.0)
eps = 0.05 - eps;
}
return v;
}
float lemodule (compl_t c) {
return c.r * c.r + c.i * c.i;
}
|
White.local: a.out Avant le module 0 : 1.000000 + i 2.000000 module 0.000000 1 : 1.130000 + i 1.870000 module 0.000000 2 : 1.260000 + i 1.740000 module 0.000000 3 : 1.390000 + i 1.610000 module 0.000000 4 : 1.520000 + i 1.480000 module 0.000000 5 : 1.650000 + i 1.350000 module 0.000000 6 : 1.780000 + i 1.220000 module 0.000000 7 : 1.910000 + i 1.090000 module 0.000000 8 : 2.040000 + i 0.960000 module 0.000000 9 : 1.960000 + i 1.040000 module 0.000000 10 : 1.880000 + i 1.120000 module 0.000000 11 : 1.800000 + i 1.200000 module 0.000000 12 : 1.720000 + i 1.280000 module 0.000000 13 : 1.640000 + i 1.360000 module 0.000000 14 : 1.560000 + i 1.440000 module 0.000000 15 : 1.480000 + i 1.520000 module 0.000000 16 : 1.400000 + i 1.600000 module 0.000000 17 : 1.320000 + i 1.680000 module 0.000000 18 : 1.240000 + i 1.760000 module 0.000000 19 : 1.159999 + i 1.840001 module 0.000000 Avant le module 0 : 1.000000 + i 2.000000 module 5.000000 1 : 1.130000 + i 1.870000 module 4.773800 2 : 1.260000 + i 1.740000 module 4.615200 3 : 1.390000 + i 1.610000 module 4.524200 4 : 1.520000 + i 1.480000 module 4.500800 5 : 1.650000 + i 1.350000 module 4.545000 6 : 1.780000 + i 1.220000 module 4.656800 7 : 1.910000 + i 1.090000 module 4.836200 8 : 2.040000 + i 0.960000 module 5.083200 9 : 1.960000 + i 1.040000 module 4.923200 10 : 1.880000 + i 1.120000 module 4.788800 11 : 1.800000 + i 1.200000 module 4.680000 12 : 1.720000 + i 1.280000 module 4.596800 13 : 1.640000 + i 1.360000 module 4.539200 14 : 1.560000 + i 1.440000 module 4.507200 15 : 1.480000 + i 1.520000 module 4.500800 16 : 1.400000 + i 1.600000 module 4.520000 17 : 1.320000 + i 1.680000 module 4.564800 18 : 1.240000 + i 1.760000 module 4.635201 19 : 1.159999 + i 1.840001 module 4.731201 le plus petit est le numéro 4 1.520000 i1.480000 et son module 4.500800 |
typedef int * pint;
typedef int table [100];
void fcttab (int nb, table t) {
int i;
pint p1, p2, p3;
p3 = t;
p2 = t + 1;
p1 = t + 2;
*p3 = 1;
*p2 = 1;
for (i = 2; i <= nb; i+=1) {
*p1 = *p2 + *p3;
p3 = p2;
p2 = p1;
p1+= 1;
}
}
void seetab (table t, int nb) {
pint p;
p = t;
while (nb > 0) {
printf("%d\t", *p);
p++;
nb--;
}
printf("\n");
}
main () {
table tt;
pint pt;
int n, nbele;
n = 18;
nbele = n + 1;
/* ici, la methode classique ou tt est un tableau */
fcttab(n, tt);
seetab(tt, nbele);
n = 10;
nbele = n + 1;
/* la, la methode dynamique de "creation" d'un tableau */
pt = (pint) malloc ((size_t) (nbele * sizeof(int)));
fcttab(n, pt);
seetab(pt, nbele);
free(pt);
/* c'est plus joli, plus souple, plus dynamique */
}
|
Refaire toutes les fonctions déjà vues sur les tableaux mais avec des tableaux dynamiques.
Voici un exemple pour des tableaux d'altitude. Pour une carte, ici, un tableau carré, chaque case (une petite surface du terrain) contient son altitude. Voici l'ensemble du programme qui crée un tableau d'altitudes (la topographie d'un terrain) et l'affiche. Let's see some new types to work on the altitude field.
typedef unsigned int uint;
typedef float * tabalt ;
struct tableau {
tabalt t;
unsigned int nbc;
unsigned int nbl;
} ;
typedef struct tableau tableau;
|
tableau creetableau (uint nbc, uint nbl) {
tableau t;
t.nbc = nbc;
t.nbl = nbl;
t.t = (tabalt) malloc ((size_t) (nbc * nbl * sizeof(float)));
return t;
}
|
void puttab (tableau t, uint i, uint j, float amettre) {
if (i < t.nbc && j < t.nbl) {
*(t.t + i + j * t.nbc) = amettre;
}
}
float valtab (tableau t, uint i, uint j) {
if (i < t.nbc && j < t.nbl) {
return *(t.t + i + j * t.nbc);
}
return -1.0;
}
|
void remplirtab (tableau t) {
uint i, j;
float val;
for (i = 0; i < t.nbc; i++)
for (j = 0; j < t.nbl; j++) {
val = (float) (30 * i + 20 * i * j + 15 * j);
while (val > 2000.0)
val = val - 2000.0;
if (val > 1000.0)
val = 2000.0 - val;
puttab(t, i, j, val);
}
}
|
void voirtab (tableau t) {
uint i, j;
for (j = 0; j < t.nbl; j++) {
printf ("%6d", j);
}
printf("\n");
for (i = 0; i < t.nbc; i++) {
printf ("%4d |", i);
for (j = 0; j < t.nbl; j++) {
printf ("%6.2f ", valtab(t, i, j));
}
printf("\n");
}
}
|
int main () {
uint sx, sy;
tableau t;
sx = 10;
sy = 10;
t = creetableau (sx, sy);
remplirtab (t);
voirtab(t);
}
|
0 1 2 3 4 5 6 7 8 9 0 | 0.00 15.00 30.00 45.00 60.00 75.00 90.00 105.00 120.00 135.00 1 | 30.00 65.00 100.00 135.00 170.00 205.00 240.00 275.00 310.00 345.00 2 | 60.00 115.00 170.00 225.00 280.00 335.00 390.00 445.00 500.00 555.00 3 | 90.00 165.00 240.00 315.00 390.00 465.00 540.00 615.00 690.00 765.00 4 |120.00 215.00 310.00 405.00 500.00 595.00 690.00 785.00 880.00 975.00 5 |150.00 265.00 380.00 495.00 610.00 725.00 840.00 955.00 930.00 815.00 6 |180.00 315.00 450.00 585.00 720.00 855.00 990.00 875.00 740.00 605.00 7 |210.00 365.00 520.00 675.00 830.00 985.00 860.00 705.00 550.00 395.00 8 |240.00 415.00 590.00 765.00 940.00 885.00 710.00 535.00 360.00 185.00 9 |270.00 465.00 660.00 855.00 950.00 755.00 560.00 365.00 170.00 25.00 |