1. Etant donnés les mots u= aa et v= bab, écrire les mots uv, (uv)² et u³v.
2. Enoncer tous les mots de longueur 2 définis sur A.
3. Soient les ensembles
E1 = {u.v/u∈A⁺,v∈A⁺}
E2 = {u.v/u∈A⁺,v∈A^∗}
E3 = {u.v/u∈A^∗,v∈A^∗}
A quoi correspondent ces ensembles?

Le préfixe d‘un mot w est la suite de lettres u telle que il existe v et u.v=w

Le suffixe d‘un mot w est la suite de lettres u telle que il existe v et v.u=w

Un facteur d‘un mot w est le mot t, tel qu'il existe u et v et v.t.u=w

Un langage sur un alphabet A est un sous-ensemble des mots définis sur A. L

Opérations :

Union : L∪M={v/ v∈L ou v∈M}
Intersection : L∪M={v/ v∈L et v∈M}
Complémentaire : C(M)={v/ v∈ L^* et v∉M}

Le produit de deux langages A et B, est l'ensemble des concaténations de mots de A et de mots de B.

La puissance correspond au produit du même langage :

Exercice

ⁿ

Définir les langages XY, X∩ Y, X2.

Ch IV.B) Expressions Régulières

Une expression régulière est une opération sur les mots d‘un langages.

Les opérations que nous connaissons sont :

la réitération (auto-concaténation) nommée aⁿ et souvent a^* ou a⁺ (au moins un a).
la concaténation (a.b ou ab)
l'union (a|b) ou le ou, qui permet de prendre l‘une ou l‘autre des parties.

La priorité de ces opérateurs est * . |

Exemples :

(a | b) ^*.c est l‘ensemble des mots composés de a et de b et terminés par un c.
(ab | c]² est l'ensemble des mots {abab, abc, cab, aa}.

Ch IV.C) Automates

Un automate est un ensemble composé d'états (dont certains sont initiaux et d‘autres finaux), d‘un vocabulaire terminal et d‘une relation.

Nous présenterons des automates finis indéterministes (AFI) et des automates finis déterministes (AFD).

AFI

Un automate fini indéterministe est défini par un quintuplet (K, T, M, I, F ) tel que :

K est un ensemble fini d’états.
T est le vocabulaire terminal (correspondant à l’alphabet sur lequel est défini le langage).
M est une relation dans K ⇥T ⇥K, appelée relation de transition (autrement dit, M est un ensemble de triplets de la forme (Si, a, Sj ) où Si et Sj sont des états de K et a est un symbole du vocabulaire terminal T ). Intuitivement, un triplet (Si, a, Sj ) 2M signifie que si l’automate se trouve dans l’état Si et le mot à analyser commence par le symbole a, alors l’automate peut aller dans l’état Sj.
I ✓K est l’ensemble des états initiaux.
F ✓K est l’ensemble des états finaux.

Exemple :

AFI (K, T, M, I, F )
K= {S, V, U },
T= {a, b},
M= {(S, a, S), (S, a, V ), (V, b, V ), (V, b, U )},
I= {S},
F= {U }

Il peut être dessiné sous la forme suivante :

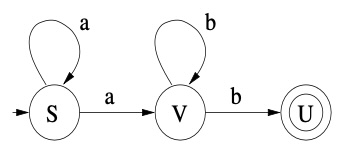
Il est indéterministe car lorsque dans l‘état S on lit un a, on ne sait pas s‘il faut changer d‘etat.

AFD

Un automate fini déterministe est défini par un quintuplet (K, T, M, S0, F ) /

K est un ensemble fini d’états.
T est le vocabulaire terminal (correspondant à l’alphabet sur lequel est défini le langage).
M est une fonction de K ⇥T dans K, appelée fonction de transition (M (Si, a) donne l’état unique dans lequel l’automate doit aller quand il se trouve dans l’état Si et que le mot à analyser commence par le symbole a).
S0 ⊂K est l’état initial.
F ⊂K est l’ensemble des états finaux.

Par exemple, l’AFD (K, T, M, S, F ) tel que
K= { S, V, U, E}
T= { a, b}
M= { (S, a) →V (S, b) →E (V, a) → V (V, b) → U
(U, a) → E (U, b) → U (E, a) → E (E, b) → E
F= { U }

est représenté graphiquement par :

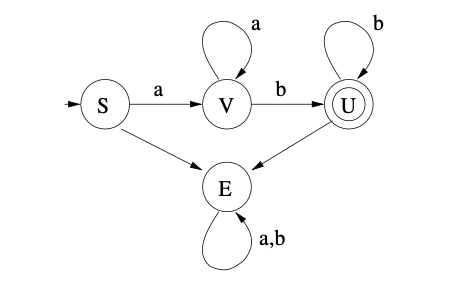
Les automates finis indéterminsites sont équivalents aux automates finis déterministes.

On trouve sur cette page, à partir de la page 19 l‘algorithme passant de l‘un à l‘autre.

Dernière mise à jour le 19/4/2025 17h00

Rajout des automates.